台形の体積(正四角錐台)の体積の求め方はどうたった?? 大きな正四角錐から小さいやつをひけばいいんだ。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。底面が1辺8cmの正方形で、他の辺が9cmの正四角錐OABCDの体積を求めよ。 A B C D O 9cm 8cm 底面が1辺12cmの正方形で、他の辺が10cmの正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積
シンプソンの公式 応用編 Fukusukeの数学めも
正四角錐の体積 公式
正四角錐の体積 公式-三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。 (2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。 いらない部分は全て同じ形の三角錐である。である。この正四角錐の体積と表面積を求めなさ い。 体積〔〕 表面積〔〕 3〔 相似比と体積比〕 右の図の正四面体oabcで,点p,q, rは辺oa,ob,ocの中点である。この正四面体を3点p, q,rおよび,3点p,b,cを通る平面で切って3つの立体 あ,い,うに




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun
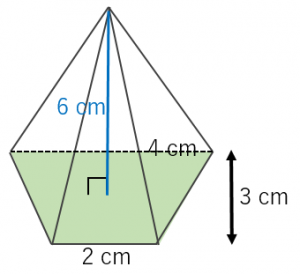
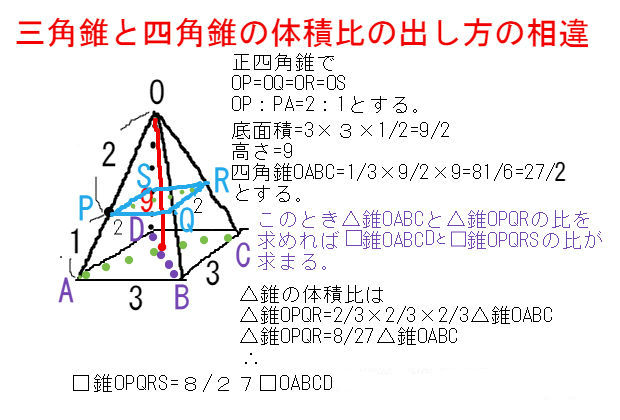
まずPともとの立体の体積比を求める P:もと=23 33 =8 27 次のQの体積比を求める。 もと -P 体積比27 体積比8 =Q 体積比19 (ウ) Pの体積が48cm3 のときQの体積を求めよ。 8 :19 P Q 体積比 = P Q 48 :x 実際の値 8 8 1 6 P x=114 答114 cm3 Q 答8 19 K 相似比と面積比と体積比-②正四角錐(底辺と高さ)|体積・表面積の計算|計算サイト 底辺の1辺の長さaが2、高さhが3の正四角錐の体積・表面積・斜辺の長さ 体積 V:4 側面積 S 1 : 表面積 S 2 : 斜辺の長さ b: 正四角錐の体積の問題になります。すべての辺の長さが2 cm である正四角錐oabcd において,辺oc 上に中点e をとる。この正四角錐の 側面上に,頂点a から辺ob と交わり点e まで線をひ くとき,最も短くなるようにひいた線の長さを求めな さい。 類題 2 1 辺が6cm の正方形abcd について,辺bc
長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。正四角錐の体積(底辺と高さから) 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘ありがとうございます。 修正致しA B C D O 15cm 12cm 底面が1辺12cmの正方形で、他の辺が15cmの正四角錐OABCDの体積を求めよ。 A B C D O 15cm 12cm O A C 15cm 15cm D A B C 12cm 12cm 点O,A,Cを通る平面で切断する。 切断面の OACは二等辺三角形
いよいよ体積 ようやく体積を求める準備が整いました。 この正四面体の高さ OH O H は下図のようになっています。 OH O H が何 cm c m なのか求めます。 当然、三角形 OAH O A H に三平方の定理を用います。 AM A M は 1 1 辺が 2cm 2 c m の正三角形の高さなので問題 右の図の正四角錐の体積と表面積を求めよ。 解 体積 1 3 ×102× 12=400 (cm3) 表面積底面積は 100 cm2。側面は合同な二等辺三角形だから, 1 2 ×10×13 ×4+100=360 (cm2) 答 体積 400 cm3,表面積 360 cm2 139 次の図の正四角錐の表面積を求めよ。三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介




角錐 円錐の体積と表面積の公式 数学fun



答3 四角錐の体積 ヤドカリの 気ままな数学
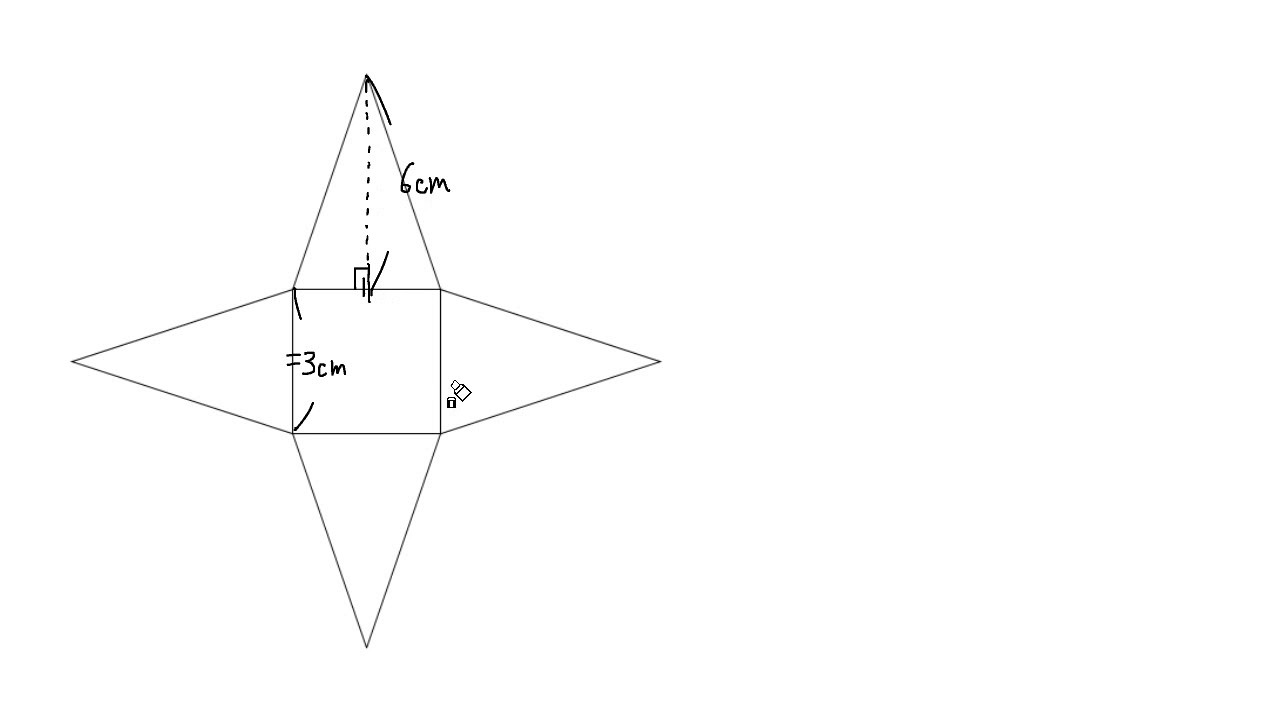
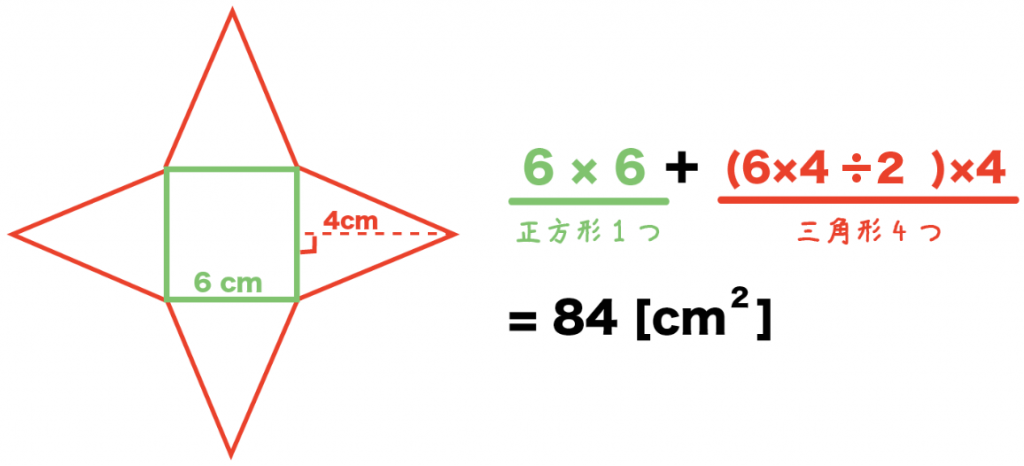
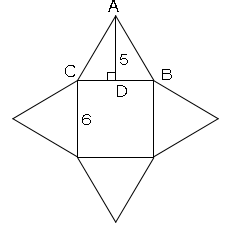
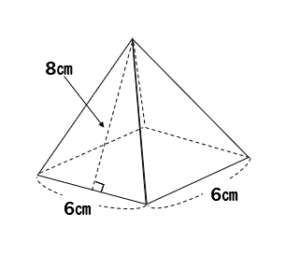
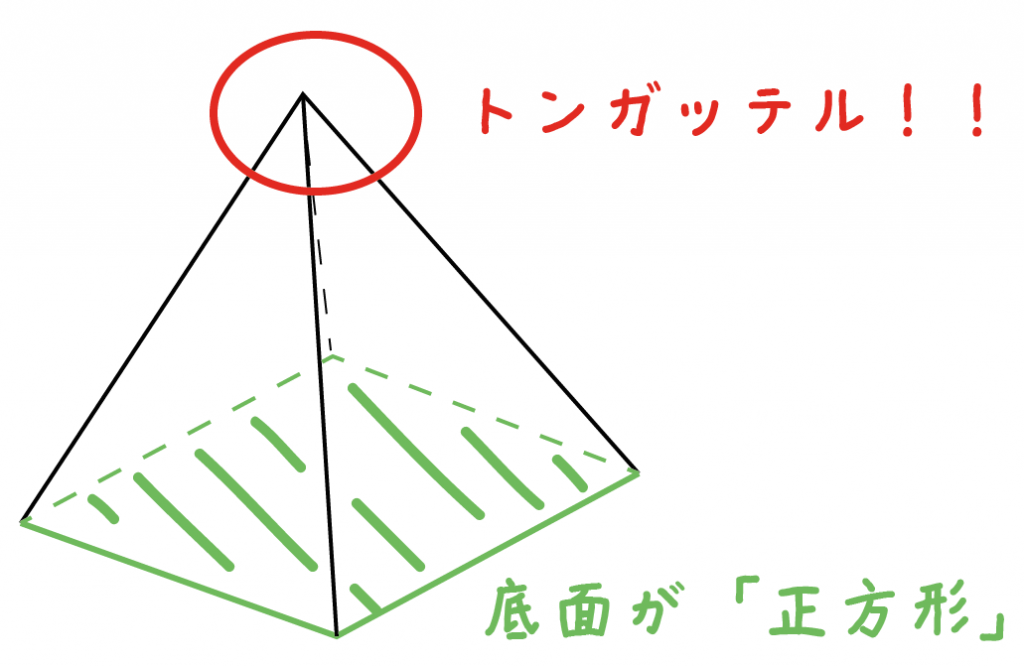
四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式 先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる って覚えておけば問題ないよ。 だから例題の正四角錐の体積は、 6×6×8×1/3 = 96 cm³ になるんだ。 おめでとう! これで正四角錐の体積を計算できたね^^四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でも 正四角錐の体積




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



正四角錐の表面積 Youtube
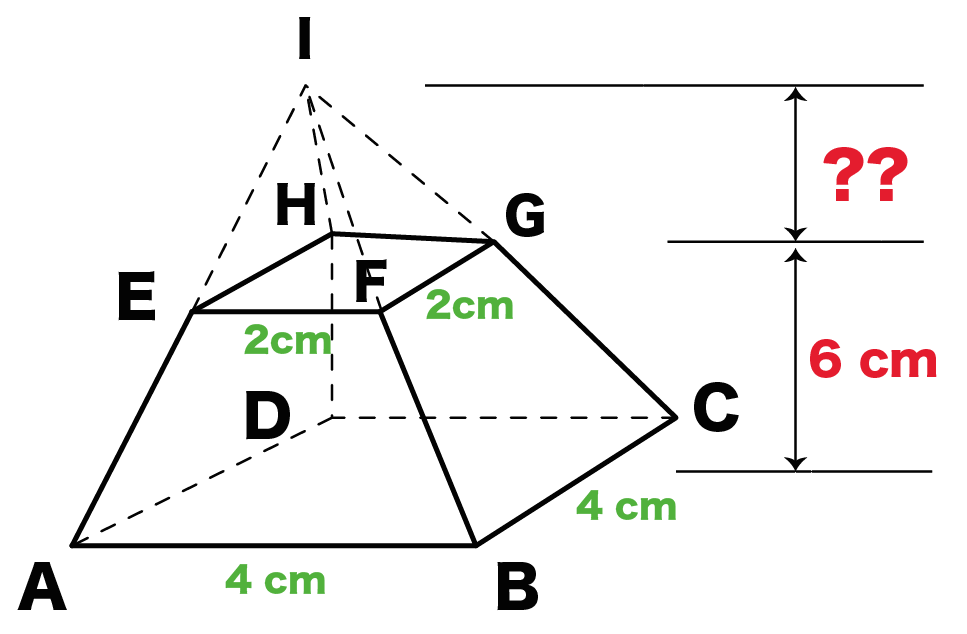
図は底面が正方形の正四角錐で、底面の正方形は1辺6cm,四角錐の高さは8cmである。 OCの中点がP、DCの中点がF、CE=2cmである。 このとき三角錐 PAEF の体積を求めよ。数学 図形 三平方の定理 正四角錐 から,考え方をお伝えしております。ぜひ身につけておこう! 正三角錐・正四面体の計算方法 体積V = 1辺の長さの3乗 ÷ 12 × √2 表面積 = 1辺の長さの2乗 × √3 正三角錐は1つの辺の長さで計算ができます。 √2と√3は無理数のため、小数点以下は延々と続きます。 当サイトではGoogle計算機より求められる √2=




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



1
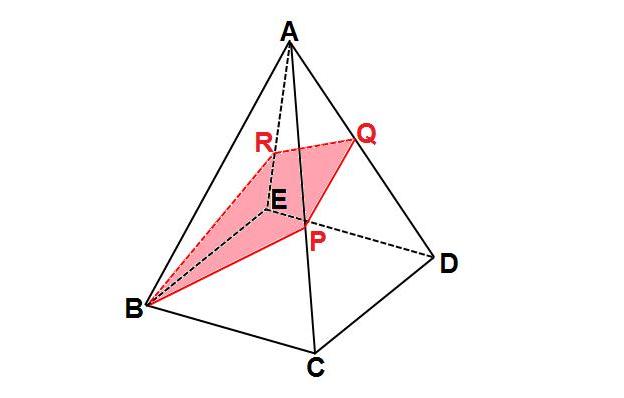
正方形abcdの対角線の交点をhとする。 pacはpa=pcの二等辺三角形なのでph⊥acである。 ac=6 2 よりah = 3 2 、pa=3 6 三平方の定理より ph 2 18 = 54 ph = 6 体積を求める。 正方形abcd = 6×6 = 36 pabcdの体積は 36×6÷3=72 pabの面積を求める。 pa=pb=3 6 、ab=6なので ∠apb=θとすると図のように底面が1辺2cmの正方形で,他の辺が の正四角錐oabcd に球が内接しています。このとき,次の問いに答えなさい。 (1)正四角錐oabcd の体積を求めなさい。 (2)正四角錐oabcd の表面積を求めなさい。 (3)内接している球の半径を求めなさい。下図のような正四角錐oabcdがあり、その辺の長さはすべて6cmです。 oaを2:1に内分する点をpとします。 qはoc上を動きます。 平面bpqとodとの交点をrとします。 問題1 oq:qc=1:2の時、四角錐opbqrの体積を求めてください 問題2



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




直撃 中学入試 第135回 筑波大附属中 立体 正四角錐の切断 北辰塾 情報局
四角錐 体積 公式 5 底面が正方形で、正四角錐なので、底面の対角線の交点上に高さとなる垂線は下りてきます。, (2) どなたか、簡単な説明方法を教えてください。 ちなみに負かけ正、正かけ負の計算は理解できています。 この問題の円錐の表面積を この立方体の中心Oを頂点としてできる四角錐OABCDの体積を求める際には、積分は用いないで証明することができます。 この四角錐の底面積 SA S A は 4h2 4 h 2 で表すことができる。 またこの立方体の体積 V A V A は 8h3 8 h 3 で表すことができる。 次の正四角錐の体積を求めなさい。 正四角錐の体積を求めるためには $$(体積)=(底面積)\times \color{red}{(高さ)}\times \frac{1}{3}$$



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ



1
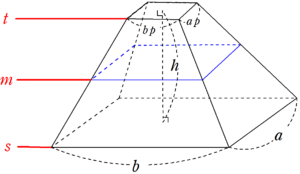
正四角錐の底面が正四角形です。底辺の長さ (a) が等しいです。縦辺の長さ (b) も同等です。側面が二等辺の三角形です。正角錐の高さの基点が底面の中心と一致します (O) 。 角錐の側の面が側面を形成します。正四角錐の場合は、側面が二等辺の三角形です。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式! ? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、体積 V = h 6 ( a d b c 2 ( a b d c))
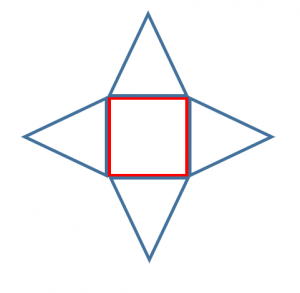



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




三平方の定理の利用 四角錐 円錐 チーム エン
右の図の正四角錐の体積と表面積を求めよ。 解 底面積は,10 =100 cm より, 体積は, 1 3 ×100×12=400 (cm3) 側面積は, 1 2 ×10×13 ×4=260 cm より, 表面積は,=360 (cm2) 160 次の角錐の体積を求めよ。また,⑶については表面積も求めよ。要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます.さて、正四角錐を平面oacで2分割します。 三角錐A-COD と 三角錐AROS の 高さ は共通だから、 体積比 は 底面 の 面積比 に等しい。 よって、
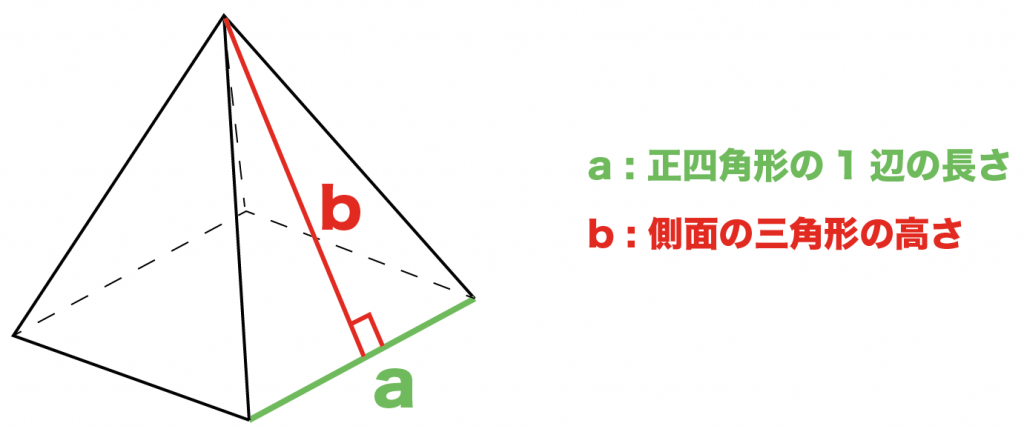



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立体の体積 無料で使える中学学習プリント
正四角錐の体積 = 64×7÷3 = 448 3 cm 3 つぎの立体のの体積を求めよ。 母線の長さ 13cm, 底面の半径5cmの円錐 母線の長さ 6cm, 底面の半径4cmの円錐 母線の長さ 7cm, 底面の半径2cmの円錐 底面が1辺12cmの正方形で、他の辺が11cmの正四角錐 底面が1辺4cmの正方形で、他の正四角錐の高さを含む直角三角形に注目、三平方の定理から高さを求める。 ②で求めた高さを用いて、体積の公式に当てはめて計算する。 練習問題に挑戦しよう!問題 次の正四角錐の体積を求めなさい。 解説&答えはこちら 四角錐の展開図 新興




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




四角錐台の体積 高精度計算サイト
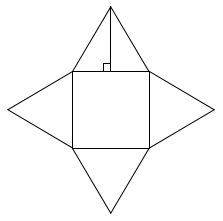



正四角錐の体積の問題 数学の要点まとめ 練習問題一覧




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ



第57問の解答




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



第57問の解答
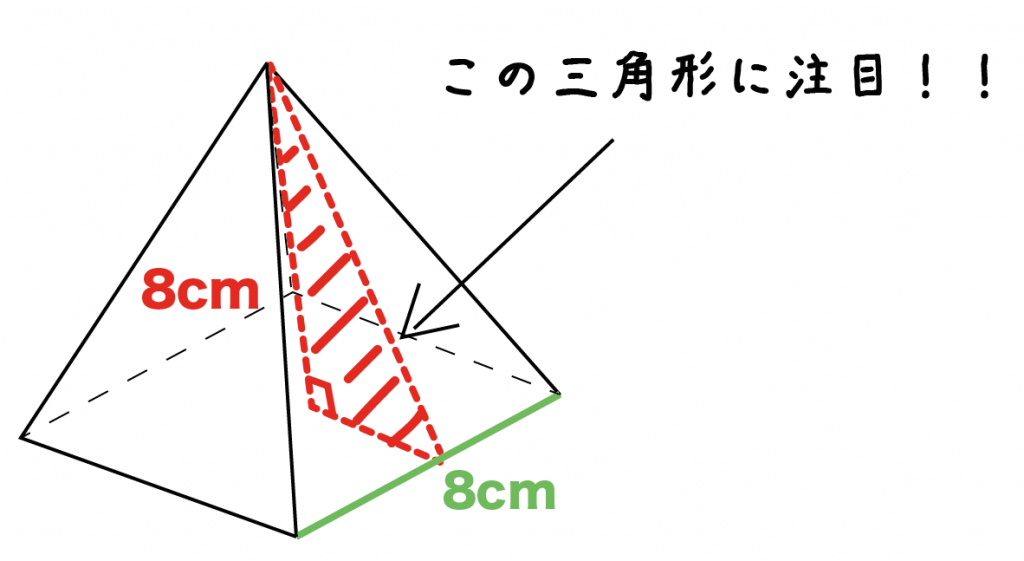



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




正四角錐の表面積と体積の求め方を教えてください Clear
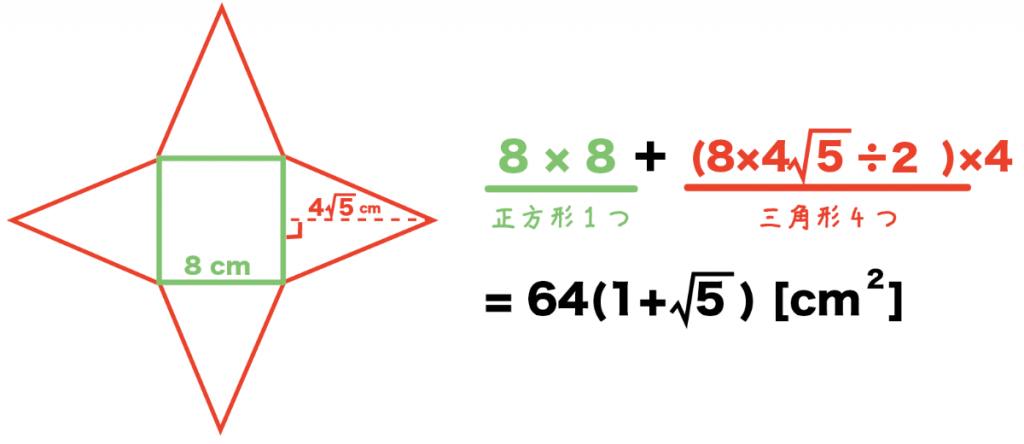



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
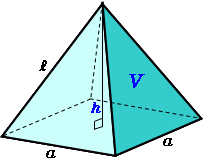



正四角錐の体積 底辺と側辺から 高精度計算サイト



正四角錐の体積の問題 数学の要点まとめ 練習問題一覧




四角錐の体積の求め方 公式 小学生 中学生の勉強



一辺の長さをaとする正四角錐の体積はどのように求めればいいのでしょうか Yahoo 知恵袋




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア




四角錐の体積の求め方 公式 小学生 中学生の勉強



辺の長さが全て4である正四角錐がある P Qは中点である このと Yahoo 知恵袋



悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



Studydoctor正四角錐と三平方の定理 中学3年数学 Studydoctor



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




どうして1 3なの 錐の体積の公式の求め方 まなべーと




四角錐の表面積の求め方 公式 小学生 中学生の勉強



1



三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト



計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
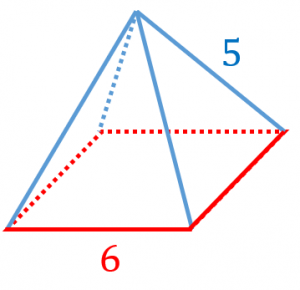



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



中学数学です 写真は 正四角錐の展開図である この展開図からできる正四 Yahoo 知恵袋
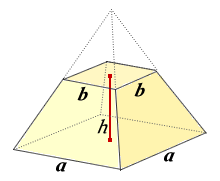



みんなの知識 ちょっと便利帳 正四角錐台の体積を計算する




この体積と表面積の求め方を教えてください Clear
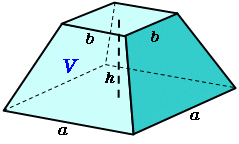



正四角錐台の体積 高精度計算サイト




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



1



第87問の解答




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
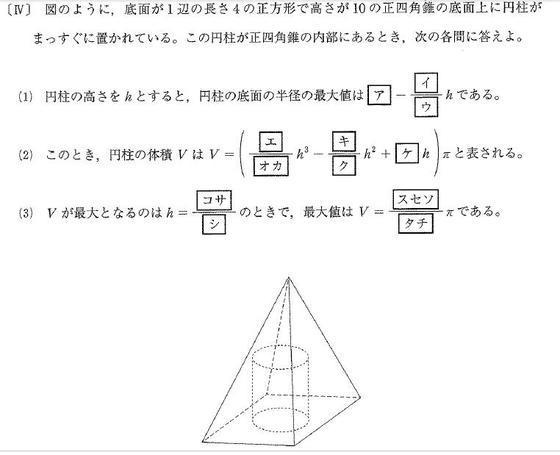



正四角錐に内接する円柱の体積の最大問題です 大学入試数学問題の解説 解答




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
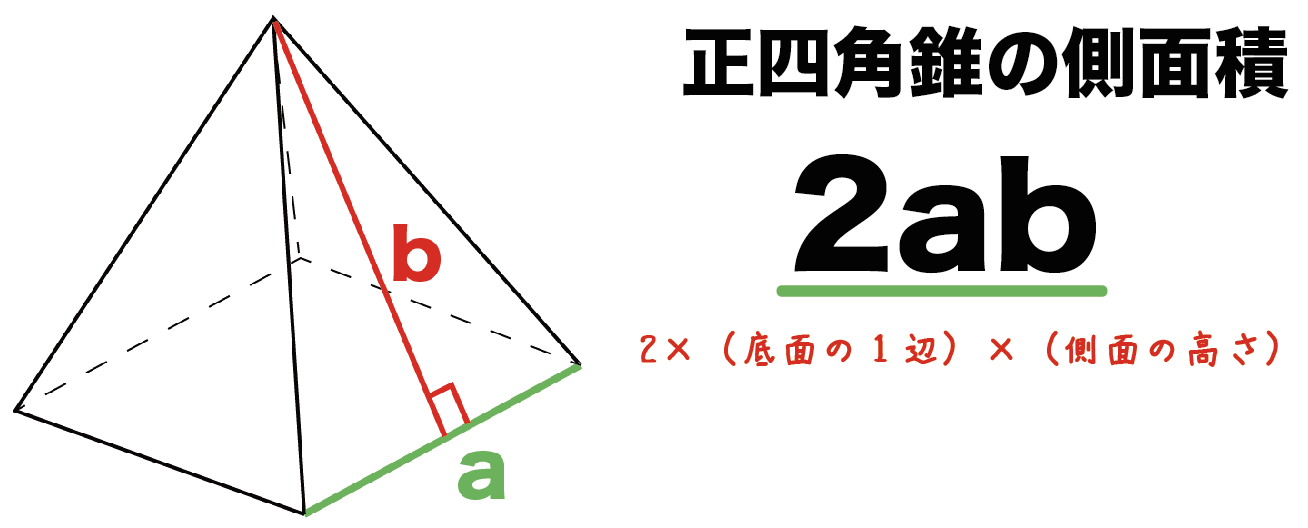



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
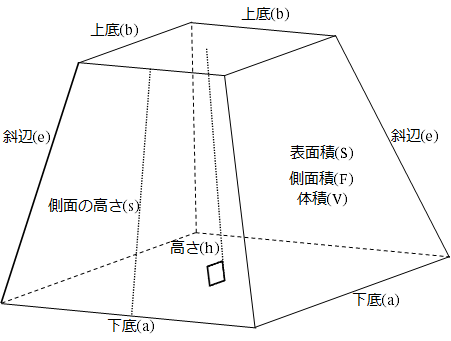



Excelワークシート 正四角錐台の体積や表面積などを計算するワークシート 黒い箱の中




誰でもわかる数学 中学1年 立体の体積 角錐 円錐 Youtube




数学 中3 54 相似と体積 基本編 Youtube




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




正四角錐3つから正四角柱1つがつくれる 中1 空間図形の体積 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles
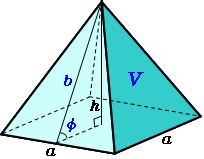



正四角錐の体積 底辺と高さから 高精度計算サイト




角錐と円錐の体積 Youtube



中1数学 体積の問題 底面の一辺の長さがacm 高さがh Yahoo 知恵袋




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703




正四角錐と三平方の定理 中学3年数学 Youtube
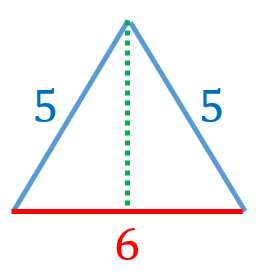



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




角錐の体積 底面が1辺6センチの正方形で他の辺が5センチの正四角錐が 数学 教えて Goo




高校入試 三角錐と四角錐の切断 Youtube




5 1 A Cm H Cm Descubre Como Resolverlo En Qanda



この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋




四角錐の体積の求め方 公式 小学生 中学生の勉強




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




シンプソンの公式 応用編 Fukusukeの数学めも



四角錐の体積



Math 角錐の体積が角柱の3分の1になる証明 働きアリ The 2nd



超難問 正四角錐の切断面の面積と切断立体の体積 中学数学 理科 寺子屋塾の復習サイト



正四角錐の体積の求め方や高さの求め方などがわかりません教えてください Yahoo 知恵袋



正四角錐の体積の問題 数学の要点まとめ 練習問題一覧
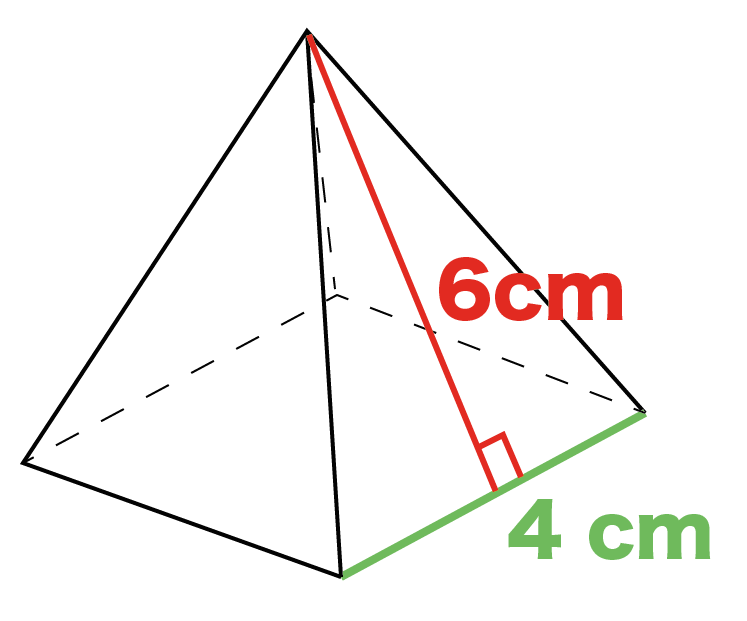



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




四角錐の体積の求め方 公式 小学生 中学生の勉強




角錐 円錐の体積 Youtube




四角錐 円錐の体積 チーム エン



この正四角錐の展開図から正四角錐の体積の求め方を教えてください 答えは Yahoo 知恵袋



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
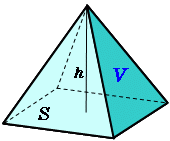



角錐の体積 高精度計算サイト




三平方の定理でこの正四角錐の体積を求めるのですが Clear




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
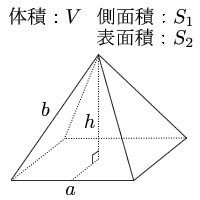



正四角錐 底辺と高さ 体積 表面積の計算 計算サイト




56 四角錐の切断と体積 Youtube




正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




どうして1 3なの 錐の体積の公式の求め方 まなべーと




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿