That is a circle floating 25 feet in the air The intersection of z = x 2 and z = 25 − y 2 is z = x 2 = 25 − y 2 or x 2 y 2 = 25 = z y 2 That is a horse on a merrygoround The horse's pole goes around in a circle while the horse itself goes up and down REBOOT (you can see my earlier posts in the edit) Solve the system of conic sections Involves the elimination method and a graphical understanding of the solution setThere is no answer available Request an answer from our educators and we will get to it right away!
Solution X 2 25 Y 2 16 1 How To Graph That Ellipse
X^2+y^2=25 is written in polar form as
X^2+y^2=25 is written in polar form as-Simple and best practice solution for x^2y^225=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itX^{2}y^{2}2 x4 yk=0 passes through (a) k=0 (b) k=1 (c) k=15 (d) k=1 (p) (3,4) (q) (1,2) (r) (0,0) (s) (0,4) Uh oh!




Solution What Is The Equation Of The Normal To The Curve X 2 Y
Click here👆to get an answer to your question ️ The equation of a tangent to the circle x^2 y^2 = 25 passing through ( 2, 11 ) isContact Pro Premium Expert Support »Solution for X^2y^225=0 equation Simplifying X 2 y 2 25 = 0 Reorder the terms 25 y 2 X 2 = 0 Solving 25 y 2 X 2 = 0 Solving for variable 'y' Move all terms containing y to the left, all other terms to the right Add '25' to each side of the equation 25 25 y 2 X 2 = 0 25 Combine like terms 25 25 = 0 0 y 2 X 2 = 0 25 y 2 X 2 = 0 25 Combine like terms 0 25 = 25 y
Clearly, A is the set of all points on the circle x 2 y 2 = 2 5 and B is the set of all points on the ellipse x 2 9 y 2 = 1 4 4 These two intersect at four points P, Q, RFind the value of 4 x 2 y 2 25 z 2 4 x y − 10 y z − z x when x = 4, y = 3 and z = 2 Please scroll down to see the correct answer and solution guide Right Answer is\frac{ { x }^{ 2 } }{ 4 } \frac{ { y }^{ 2 } }{ 25 } =1 − 4 x 2 2 5 y 2 = 1 Multiply both sides of the equation by 100, the least common multiple of 4,25
Find the equation of the tangent to each circle $ x^2 y^2 = 25 $ at the point $(3;4)$ asked in Mathematics by ♦ adminTedsf Wooden ( 2,066 points) 59 views geometryThere is no answer available Request an answer from our educators and we will get to it right away!Solution for X^2y^22xy=25 equation Simplifying X 2 y 2 2xy = 25 Reorder the terms X 2 2xy y 2 = 25 Solving X 2 2xy y 2 = 25 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '2xy' to each side of the equation



Solution X 2 25 Y 2 16 1 How To Graph That Ellipse



Search Q X 5e2 Y 5e2 3d0 Tbm Isch
Graph (x1)^2 (y2)^2=25 (x − 1)2 (y − 2)2 = 25 ( x 1) 2 ( y 2) 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of theSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreClick here👆to get an answer to your question ️ Given R = {(x, y) x, y ∈ W, x^2 y^2 = 25} , where W is the set of all whole numbers Find the domain and range of R
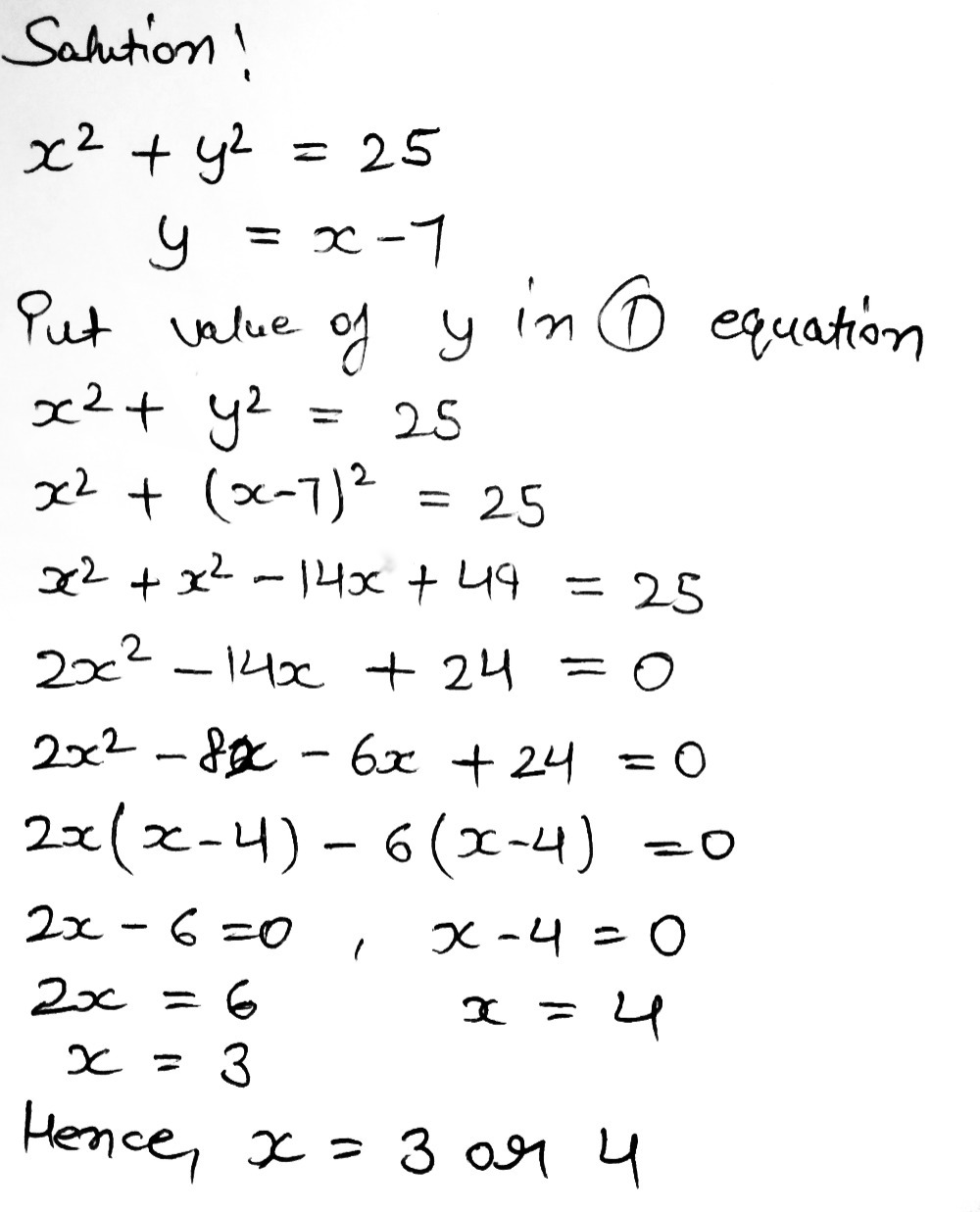



7 Solve The Simultaneous Equations X2 Y2 25 Y X Gauthmath




Find The Equation Of The Tangent Line To The Curve Implicit Differentiation Mathematics Stack Exchange
X2y2=25 Simple and best practice solution for X2y2=25 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itAnna from SVSU Micro Math helps you graph an ellipseProblem Graph the ellipse x^2/4 y^2/25 = 1Level intermediate/college algebra#SVSUmicromathX^2y^2=25 Calculadora passo a passo Symbolab Calculadoras gratuitas passo a passo para álgebra, trigonometria e cálculo This website uses cookies to ensure you get the best




Graph Of X 2 Y 2 25 Novocom Top
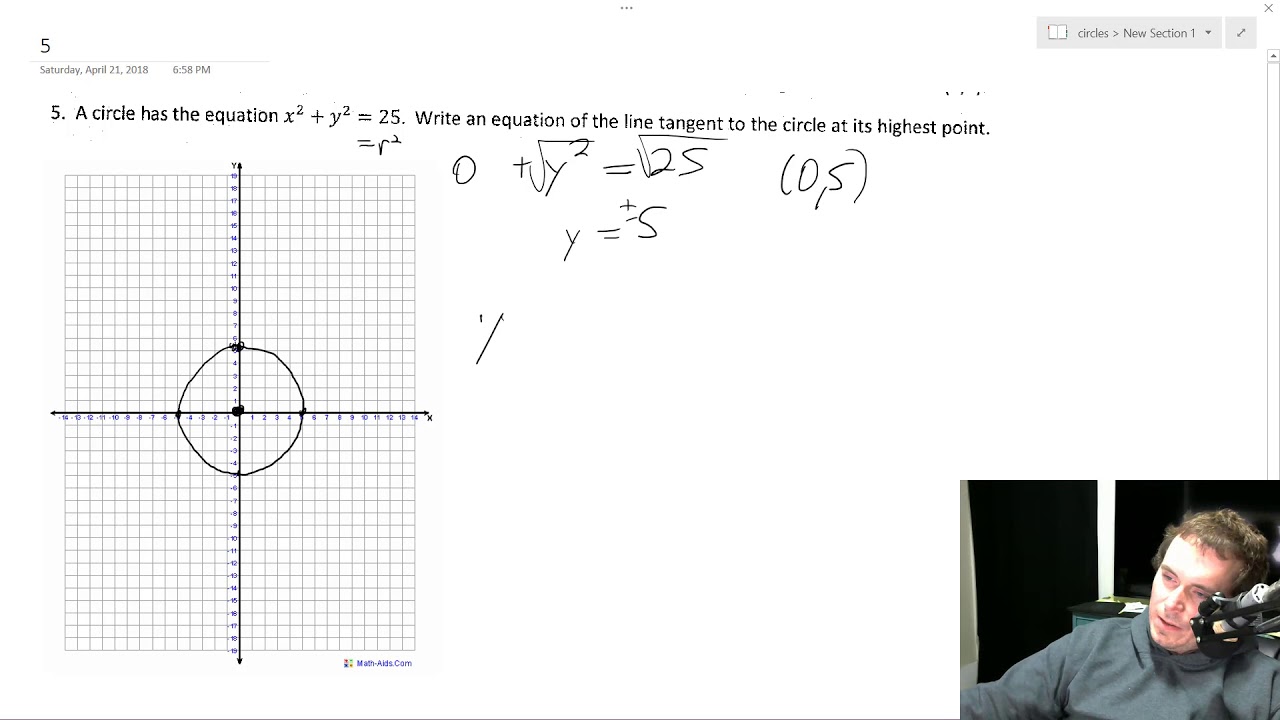



A Circle Has The Equation X 2 Y 2 25 Write An Equation Of The Line Tangent Youtube
If x = 2 for example then x 2 25 = 4 25 = 29 which is a prime number Thus the only factors of 29 are 29 and 1 and hence the only factorization of 29 is 29 × 1 Similarly if x = 4 then x 2 25 = 41 which is again prime Hence the only factorization of x 2 25 which is valid for every number x is x 2 25 = (x 2 25) × 1Let R = (x, y) x, y ϵ Z and x 2 y 2 = 25} Express R and R –1 as sets of ordered pairs Show that R = R –1 relations;Steps Using the Quadratic Formula { x }^ { 2 } { y }^ { 2 } 2xy=0 x 2 y 2 2 x y = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions,
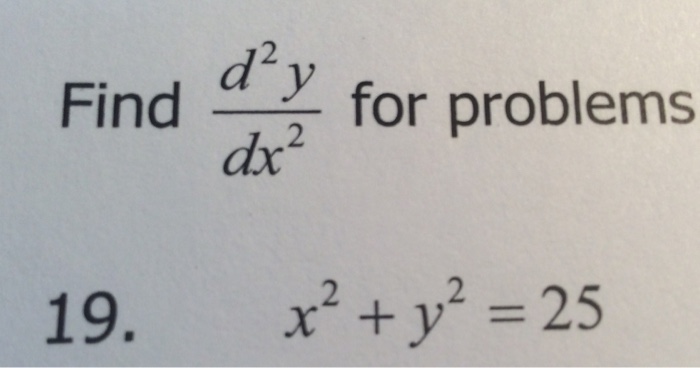



Find D 2y Dx 2 For Problems 19 X 2 Y 2 25 Chegg Com
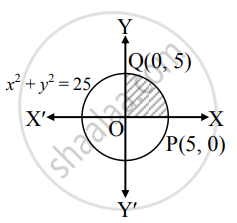



Find The Area Of Circle X2 Y2 25 Mathematics And Statistics Shaalaa Com
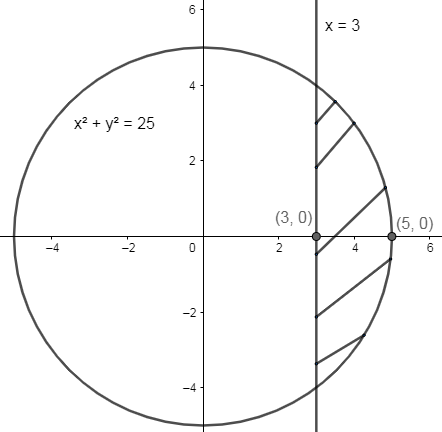
Share It On Facebook Twitter Email 1 Answer 1 vote answered 3 days ago by Harshal01 (160k points) selected 3 hours ago by Kanishk01 Best answer x 2 y 2X^2y^2z^2=1 WolframAlpha Have a question about using WolframAlpha? find the smaller area cut by the circle x^2y^2=25 by line x=3 Maths Application of Integrals



Solution X 2 25 Y 2 9 1




Please Help Urgent Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25 Brainly Com
Factor x^225 x2 − 25 x 2 25 Rewrite 25 25 as 52 5 2 x2 − 52 x 2 5 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = x a = x and b = 5 b = 5X^2y^2=25 StepbyStep Calculator Symbolab This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept StepbyStep Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Mean,(x 2) y 2 ———— —— 25 9 Step 2 x 2 Simplify —— 25 Equation at the end of step 2 x 2 y 2 —— —— 25 9 Step 3 Calculating the Least Common Multiple 31 Find the Least Common Multiple The left denominator is 25 The right denominator is 9




Example 1 A If X2 Y2 25 Find Dy Dx B Find An Chegg Com
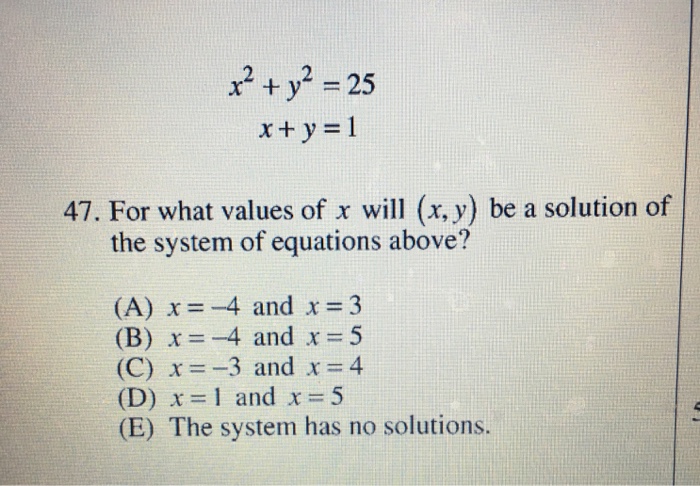



X 2 Y 2 25 X Y 1 For What Values Of X Will Chegg Com
Correct option is A ( 1,3) Given that the point (λ, λ 1) lies inside the region bounded by the curve x = \(\sqrt{25y^2}\) and y axis The curve is rewritten as, ⇒ x 2 = 25 y 2 ⇒ x 2 y 2 = 25 ⇒ S = x 2 y 2 25 We know that for a point (a, b) to lie inside the circle S, the condition to be satisfied is S 11 < 0 Applying S 11 < 0 for 1 st circle,Factor x^2y^2 x2 − y2 x 2 y 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a The area of the region bounded by the ellipse x 2 /25 y 2 /16 = 1 is A π sq units B π 2 sq units C 16π2 sq units D 25π sq units



Graph X 2 Ky 2 25 For Different Values Of K



1
Simple and best practice solution for x^22xyy^2=25 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkGiven equation of curve {eq}2(x^2 y^2)^2 = 25(x^2 y^2) {/eq} We have to find the equation of the tangent line to the curve at (3, 1) We are going to use following three rules to find slopeX2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k




Express X Y X 2 Y 2 25 Where X Y Inw As A Set Of Orde




Convert The Rectangular Equation To Polar Form And Select Its Graph X 2 Y 2 25 Study Com
For Guidance Contact anilanilkhandelwal@gmailcom Click here 👆 to get an answer to your question ️ x = 5 x ^ 2 y ^ 2 = 25 show work alsoGraph x^2y^2=25 x2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form



If The Eccentricities Of Two Ellipse X 2 169 Y 2 25 1 And X 2 A 2 Y 2 B 2 1 Are Equal Then A B A 5 13 Sarthaks Econnect Largest Online Education Community



The Area Of The Region Bounded By The Ellipse X2 25 Y2 16 1 Is Studyrankersonline
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers by $x^2y^2=25$,consider a very magnified neighbourhood of the curve at any point excepts the points $x=5,5$In that neighbourhood there can be defined as function $f$ such that $y=f(x)$ where $y$ satisfies the given relationNow express $y$ in terms of $x$Take one of $f(x)=\sqrt{(25x^2)}$ or $f(x)=\sqrt{25x^2}$then differentiate like a function,you will



Hyperbola X 2 25 Y 2 9 1 Youtube



Ifa X Y X2 Y2 25 Andb X Y X2 9y2 Y2 144 Thena Cap B Containsa One Pointb Four Pointsc Two Pointsd Nonecorrect Answer Is Option B Can You Explain This Answer Edurev Jee Question
Divide through by x^2y^2 Then we get, \frac{1}{y^2} \frac{1}{xy} \frac{1}{x^2} = 1 One of the denominators must be less than or equal to three x = 1 and y = 1 are ruled out Hence, xy = 2X^{2}y^{2}=25, (square of the length of the tangent from) (a) (62) (b) (5,3) (c) (4,3) (d) (0,5) (p) 0 (q) 15 (r) \overline{9} (s) 5 Uh oh!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



How Do You Write The Definite Integral To Find The Class 12 Maths Cbse




X 2 25 Y 2 4 1 Find The Vertices And Foci Of The Ellipse Youtube
Graph x^2 y^2 = 4 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features © 21 Google LLCTake the square root of both sides of the equation x^ {2}y^ {2}25=0 Subtract 25 from both sides y^ {2}x^ {2}25=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0Anna from SVSU Micro Math helps you graph a hyperbolaProblem Graph the hyperbola x^2/4 y^2/25 = 1Level intermediate/college algebra#SVSUmicromath




X 2 Y 2 25 Novocom Top




5 Solving X Y 2 25 0 And X Y 1 0 We Get The Roots Are Brainly In




Given The Ellipse X 5 2 25 Y 3 2 49 1 Homeworklib




Ellispses 1 Mathskey Com Fun Math Teaching Math Math Homework
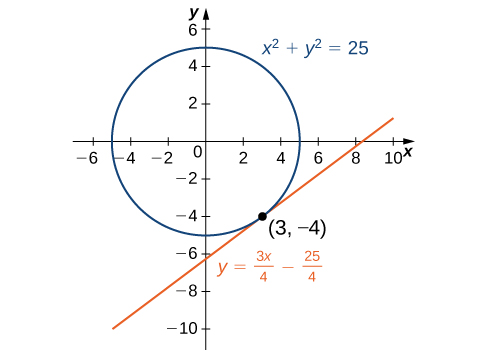



3 8 Implicit Differentiation Calculus Volume 1




Ex 11 3 2 X2 4 Y2 25 1 Find Foci Length Of Major Axis




Write The Standard Form Of The Equation For The Chegg Com
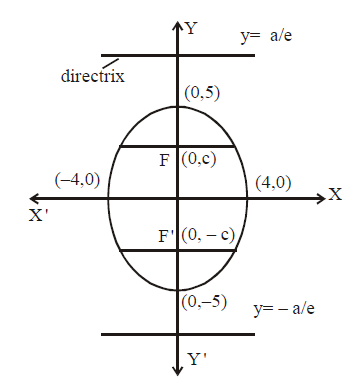



The Equation Of A Directrix Of The Ellipse X2 16 Y2 25 1 Is
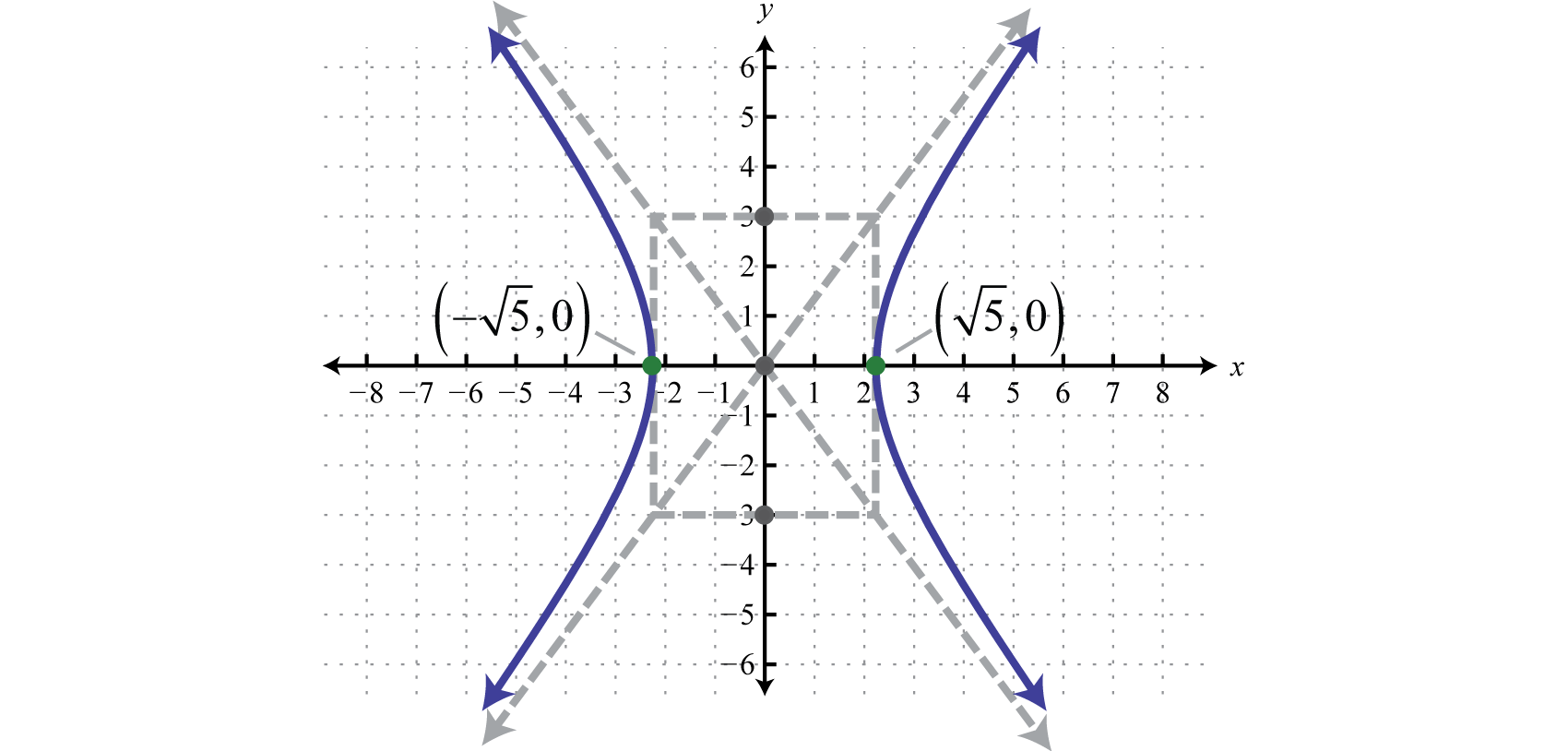



Hyperbolas



What Is The Solution To X 2 Y 2 25 Xy 12 Quora




Can You Find The Point In The First Quadrant On The Lemniscate 2 X 2 Y 2 2 25 X 2 Y 2 Where The Tangent Is Horizon X And The Value Of Y Is Unknown Quora




Find The Derivative Of X 2 Y 2 25 Using Implicit Differentiation Youtube




2 6 Implicit Differentiation Copyright Cengage Learning All




Evaluate 81x 2 36 Y 2 25 Brainly In



3 8 Implicit Differentiation Calculus Volume 1




View Question Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25
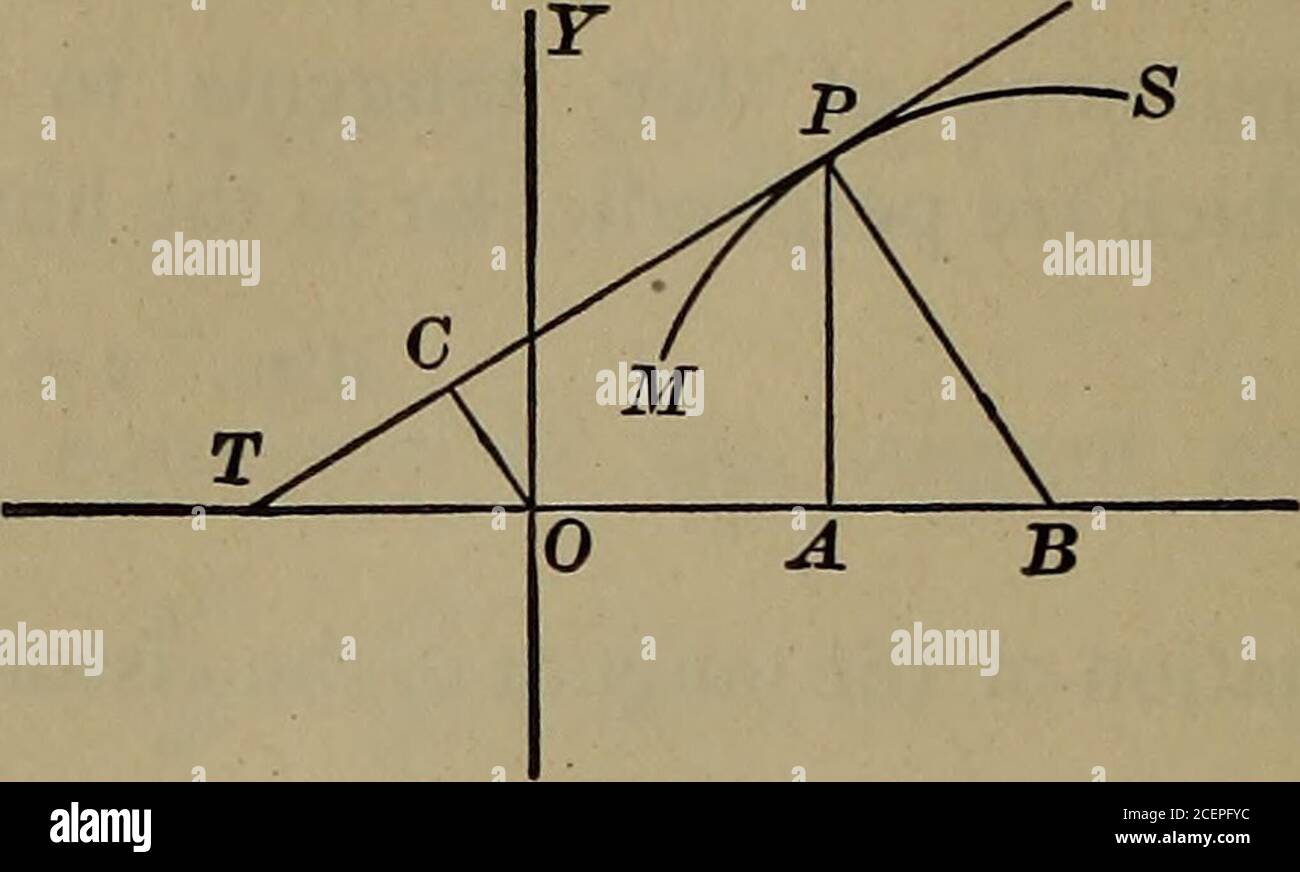



Differential And Integral Calculus To The Circle X 4 2 Y 3 2 25 At The Point 7 1 7 Find The Equations Of The Tangents To The Hyperbola4x2 Gy2 36



Search Q Equation Of A Circle Tbm Isch
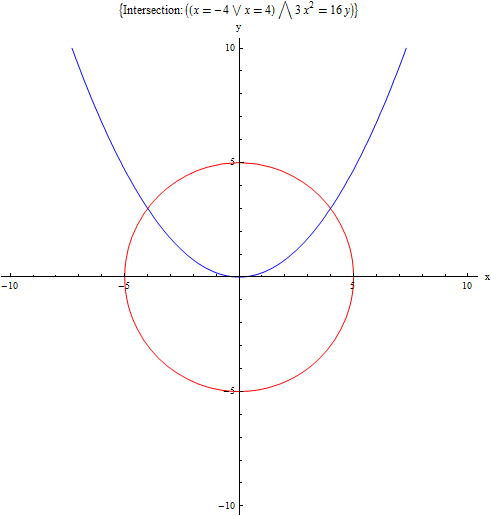



Solve The System Graphically X 2 Y 2 25 3x 2 16y 0 Homework Help And Answers Slader



1




Find The Point Of A Intersection Of Circle X 2 Y 2 25 And Line 4x 3y 12 And Also Find Length Of Intersecting Chord



What Is The Radius Of The Circle S That Touches The Hyperbola X 2 Y 2 25 In Exactly Two Places And Touches The Circle X 2 Y 2 25 In One Quora




The Two Lines Through 2 3 From Which The Circle X2 Y2 25 Intercepts Chords Of Length 8 Maths Conic Sections Meritnation Com




The Centre And Radius Of The Circle X 2 Y 2 25 Is




Solution What Is The Equation Of The Normal To The Curve X 2 Y
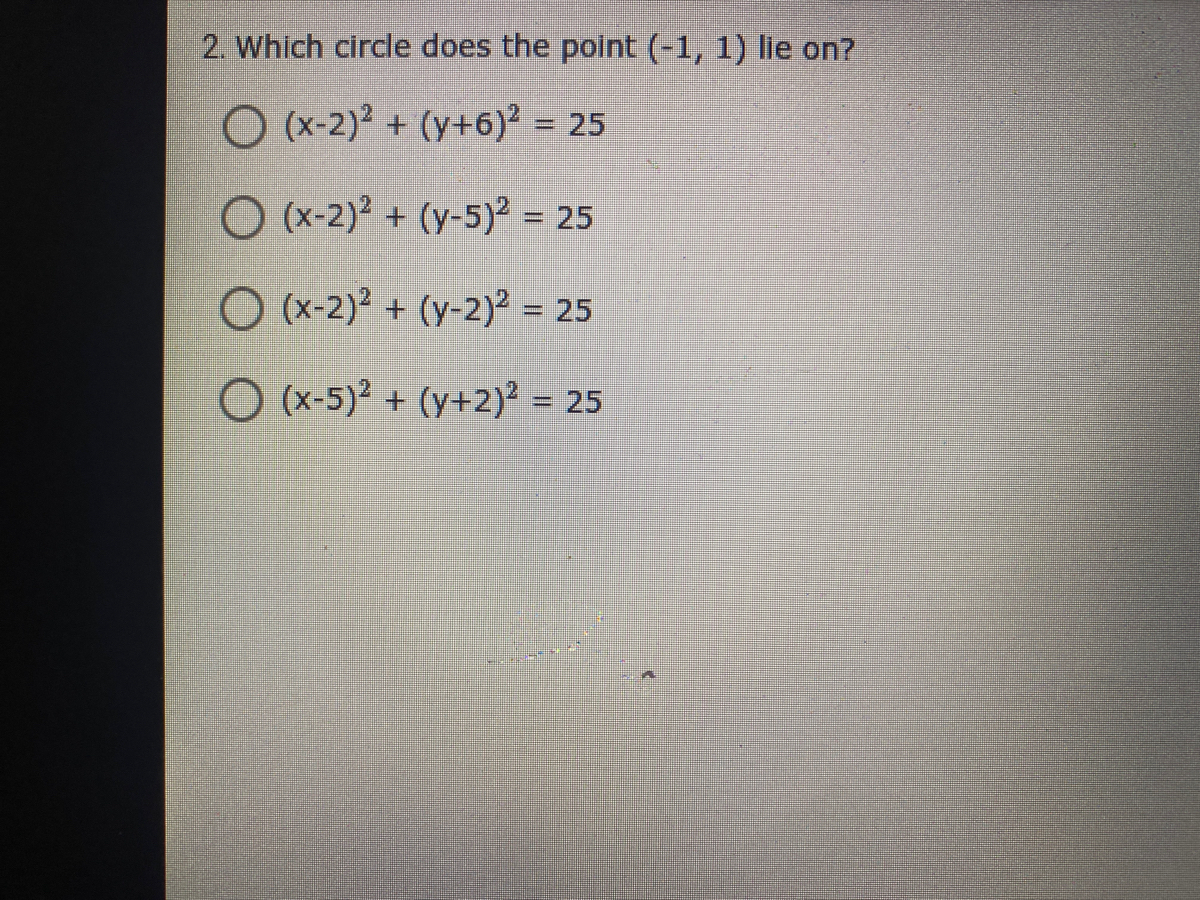



Answered 2 Which Circle Does The Point 1 1 Bartleby



Solution X2 Y2 25 Is Solving This Problem Considered A Function How Do I Plot A Graph Using A Smooth Curve For This Problem Ed



Graph X 2 Ky 2 25 For Different Values Of K



Http Www Nicolet K12 Wi Us Faculty Dgibbon Circle ellipse answer sheet pdf Pdf



Solution Stuck On How To Solve This Simultaneous Equation X 2 Y 2 25 X Y 7 Asap Please Thank You



Http Mrsaiellomath Weebly Com Uploads 3 1 4 2 86 Standard Form Of A Circle Pdf



The Equation Of A Circle Is X 3 2 Y 2 2 25 How Do You Show That The Point A 6 6 Lies On The Circle And Find The Equation Of The Tangent



Solution 3x 4y 25 X 2 Y 2 25




X 2 Y 2 25 Graph Novocom Top
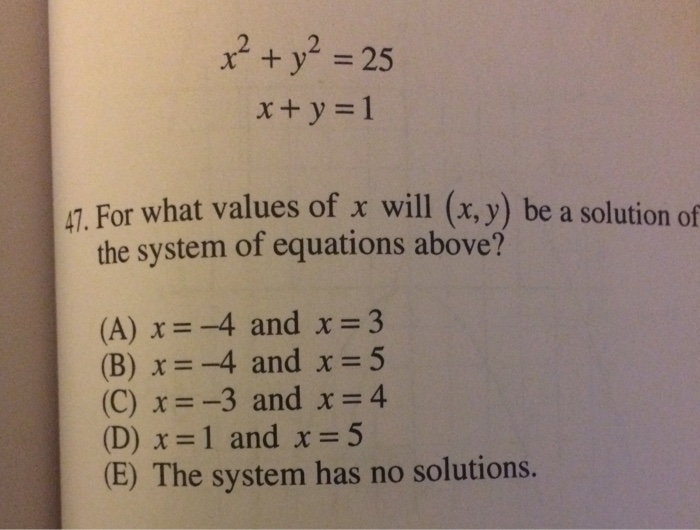



X 2 Y 2 25 X Y 1 For What Values Of X Will X Chegg Com




X 2 Y 2 25 3 4 Find The Tangent And Normal Line Youtube
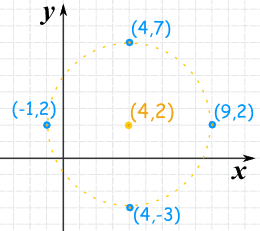



Circle Equations



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic




X 2 Y 2 25 25x 2 Y 2 25 4x 2 Y 2 4 Chegg Com
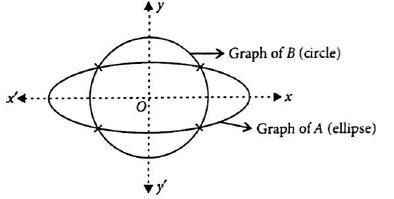



If A X Y X2 Y2 25 And B X Y X2 16y2 1




Solve System X 2 Y 2 25 Y X 2 5 Youtube



The Area Of The Region Bounded By The Ellipse X 2 25 Y 2 16 1 Is Sarthaks Econnect Largest Online Education Community




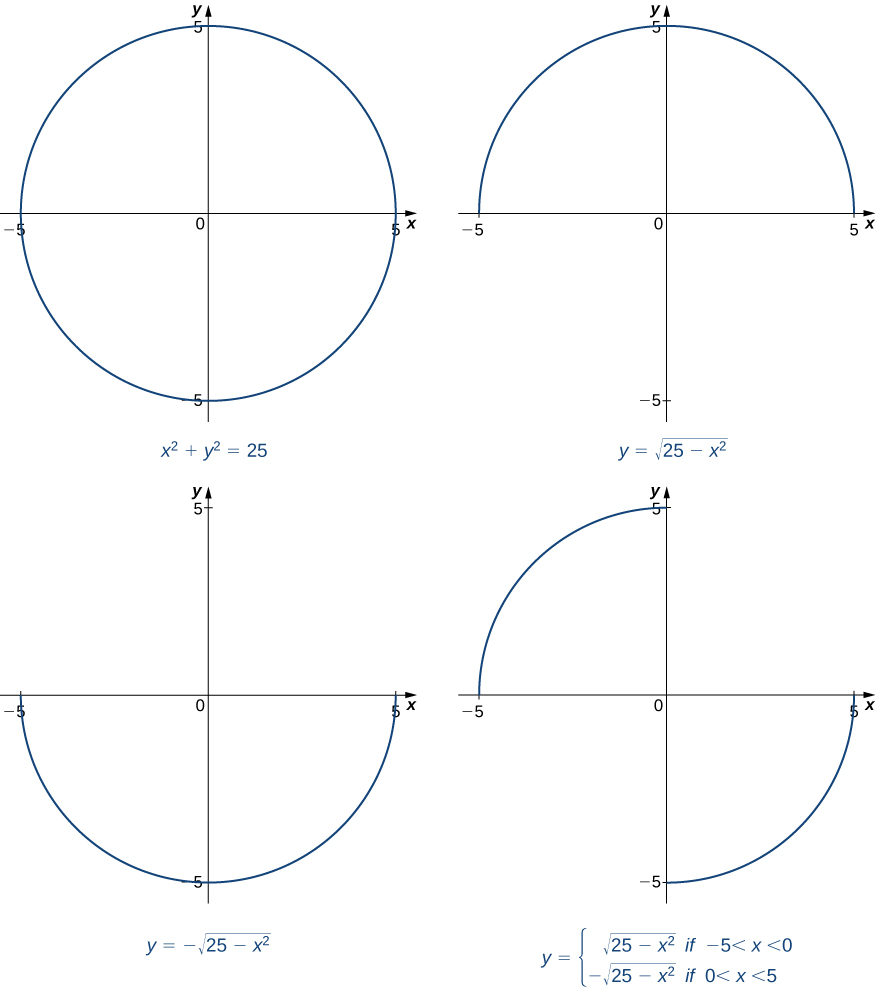
Consider The Following X Square Root 25 Y 2 0 Less Than Or Equal To Y Less Than Or Equal To 4 A Sketch The Graph Of The Function Highlighting
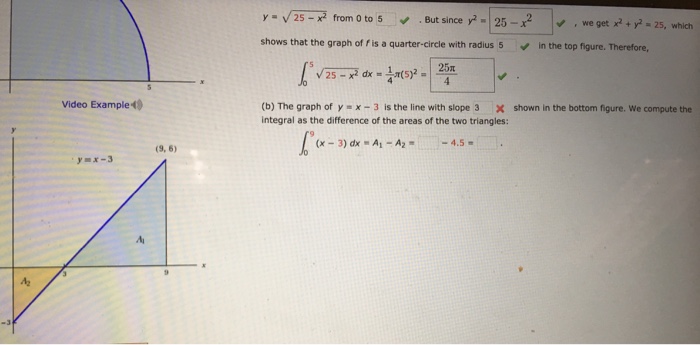



Y Squareroot 25 X 2 From 0 To But Since Y 2 Chegg Com



Solution How Do You Graph X 4 Y 2 25 What Is The Area Of The Enclosed Region



Solved Find A Vector Equation For The Tangent Lin



Graph X 2 Ky 2 25 For Different Values Of K



How Do I Find Foci Of 25x 2 16y 2 25 Mathskey Com



3 X 2 Y 2 2 25 X 2 Y 2 Implicit Differentiation Physics Forums




Solution What Is The Equation Of The Normal To The Curve X 2 Y 2 25 At 4 3




If Math X 2 Y 2 25 Math And Math X 3 Y 3 91 Math Find X And Y Quora




View Question Convert X 2 Y 5 2 25 To Polar Form



4 2 Implicit Differentiation




How Do You Find A Polar Equation For The Circle With Rectangular Equation X 2 Y 2 25 Socratic



Solution A Graph X 2 16 Y 2 25 1 Show How You Arrived At The Graph By Determining The B X Intercepts C Extent Of The Graph And The D Asymptotes Please Explain Fully I




Find The Area Of The Portion Of The Sphere X 2 Y 2 Z 2 25 Inside The Cylinder X 2 Y 2 9 Study Com




Problem Of The Day If X 2 Y 2 25 What Is The Value Of D 2 Y At The Point 4 3 Dx 2 A 25 27 C 7 27 E 25 27 B 7 27 D 3 4 Ppt Download



Solved 3d Describe And Sketch The Surface Y 2 Z 2 25 I Know What The Y 2 Z 2 25 Should Seem Like But Do Not Know What Y 2 Z 2 25 Can Anyone He Course Hero




2 1 R 2 16 R 0 0 R 2 25 R Special Pythagorean Triple Ppt Download




Consider An Ellipse X 2 25 Y 2 16 1 A Circle Passes Through A F



Http Www Nhvweb Net Nhhs Math Psorg Files 11 08 t Answers To All Conic Worksheets Pdf



Www Accessmaths Co Uk Uploads 4 4 2 3 Simultaneous Equations Quadratic Substitution Support Material Pdf
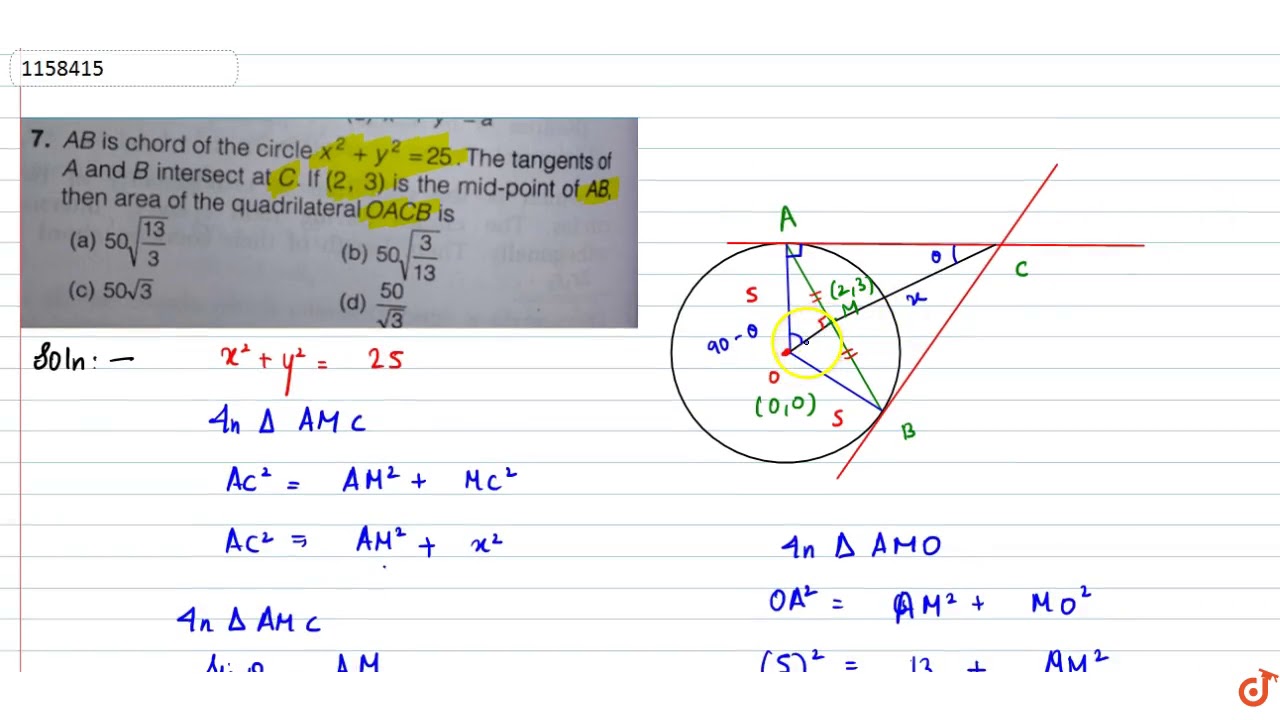



Ab Is A Chord Of The Circle X 2 Y 2 25 The Tangents Of A And B Intersect At C If 2 3 I Youtube
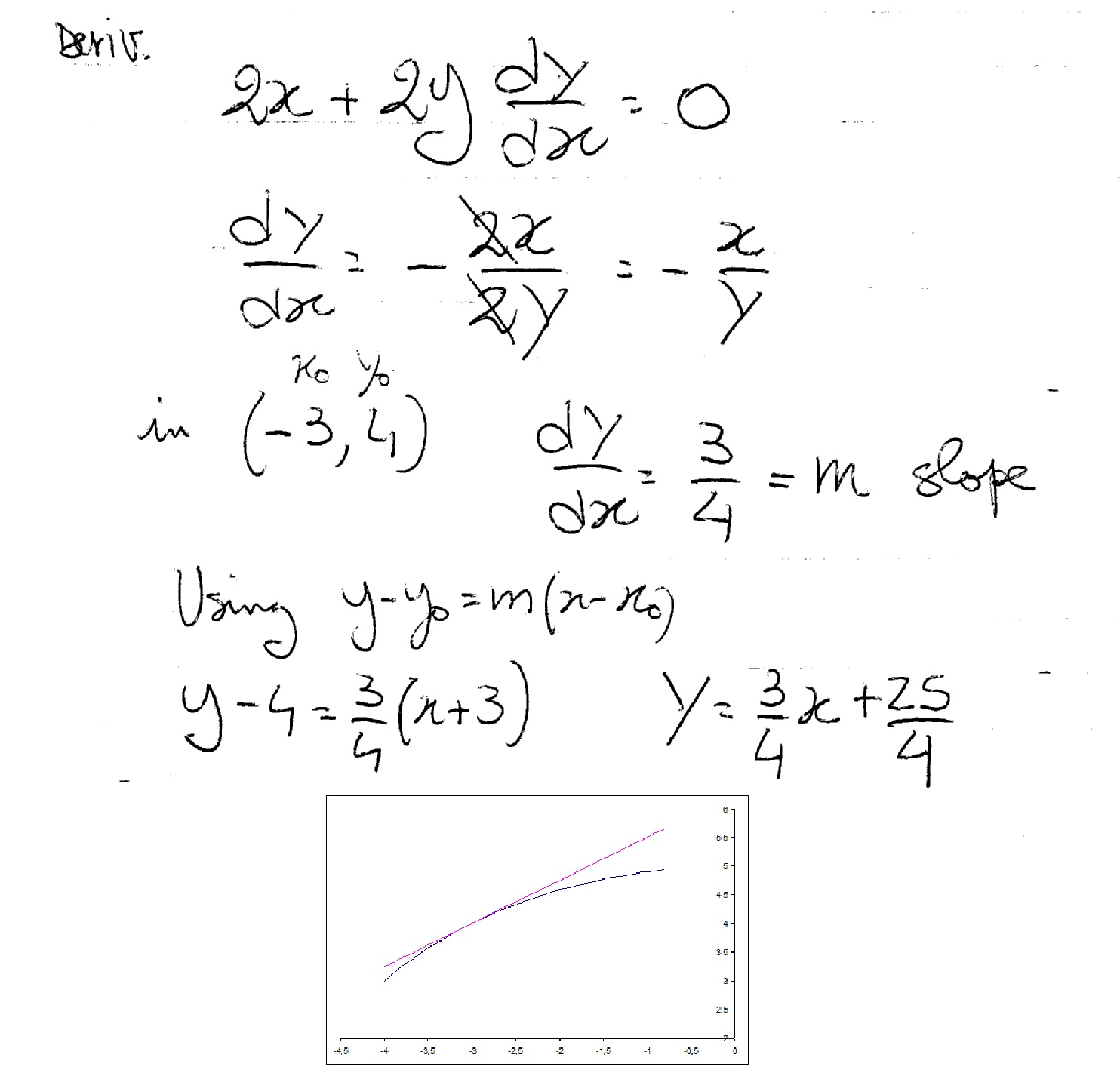



How Do You Find Equation Of Tangent To Circle X 2 Y 2 25 At The Point 3 4 Socratic
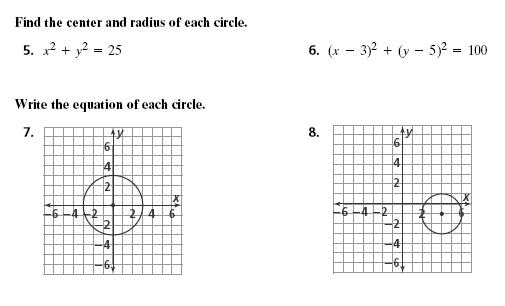



Find The Center And Radius Of Each Circle X2 Y2 Chegg Com




A Find And Identify The Traces Of The Quadric Surface X 2 Y 2 Z 2 25 Given The Plane X K Find The Trace Identify The Trace Y K




Equation For 3d Graphing Of Ellipsoid With That Has 2 Open Ends Opposite Each Other Stack Overflow



Graph Equations System Of Equations With Step By Step Math Problem Solver



Area Of X 3 2 Y 2 2 25 X Y In L 1 Cap L 2 Mathematics Stack Exchange



How To Solve The System X 2 Y 2 25 And Y 3 4x Quora



Graph X 2 Ky 2 25 For Different Values Of K




If A X Y X2 Y2 25 And B X Y X2 9y2 144 Then A B Contains Points Brainiak



Solved Find The Slope Of A Tangent Line To The Circle X 2 Y 2 25 Through The Points 3 4 Course Hero




If The Circle X A 2 Y 2 25 Intersect The Circle X 2 Y B




Implicit Differentiation
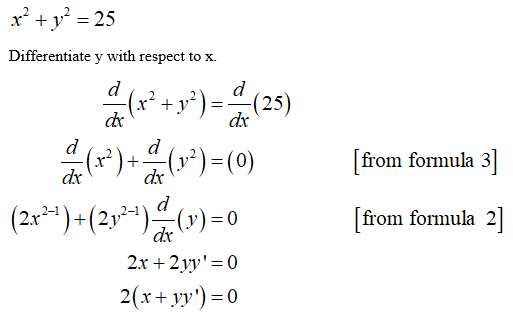



Answered Given X2 Y2 25 Find D2y Dx2 Bartleby




7 2x Y 2 25 X 2y 12 Please Factorise This The Above Question Is Different From This 7 X 2y 2 Maths Polynomials Meritnation Com



How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic



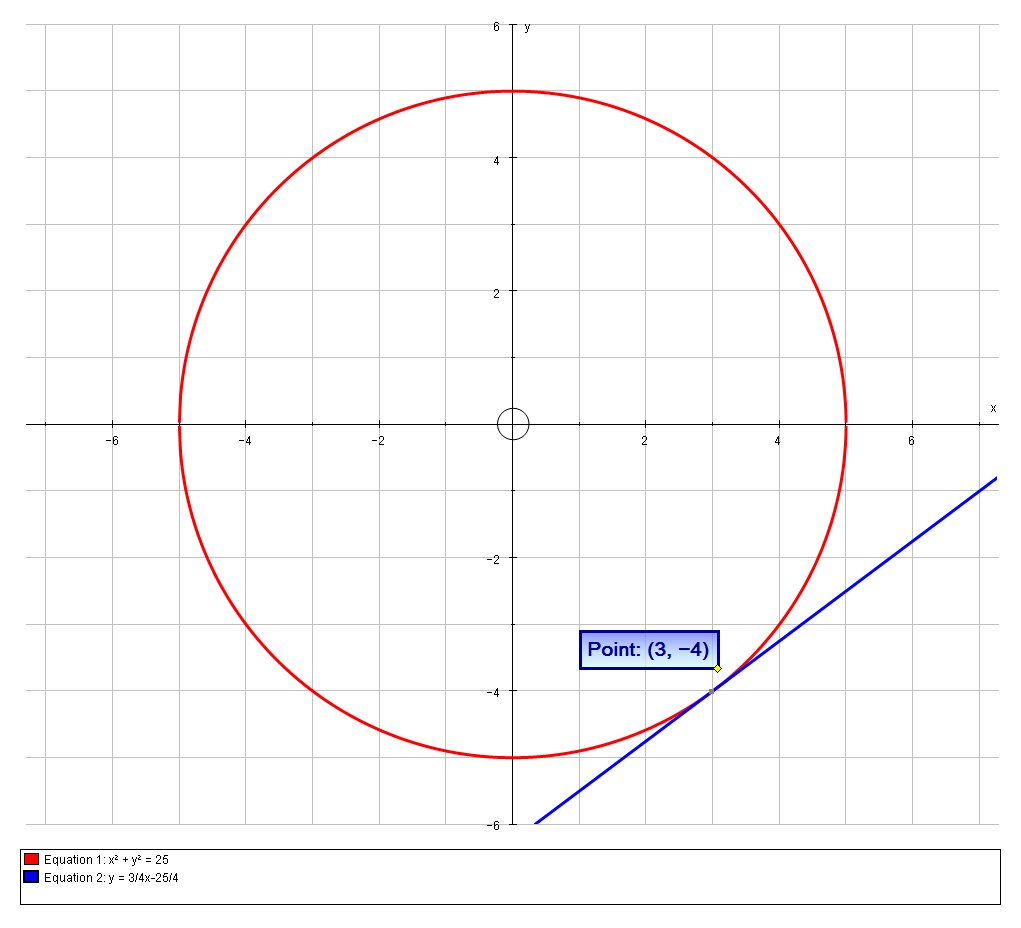
How Do You Solve X 2 Y 2 25 And Y 5 1 2x 2 Using Substitution Socratic



Www Jmap Org Worksheets A Rei C 7 Quadratic Linearsystems5a Pdf
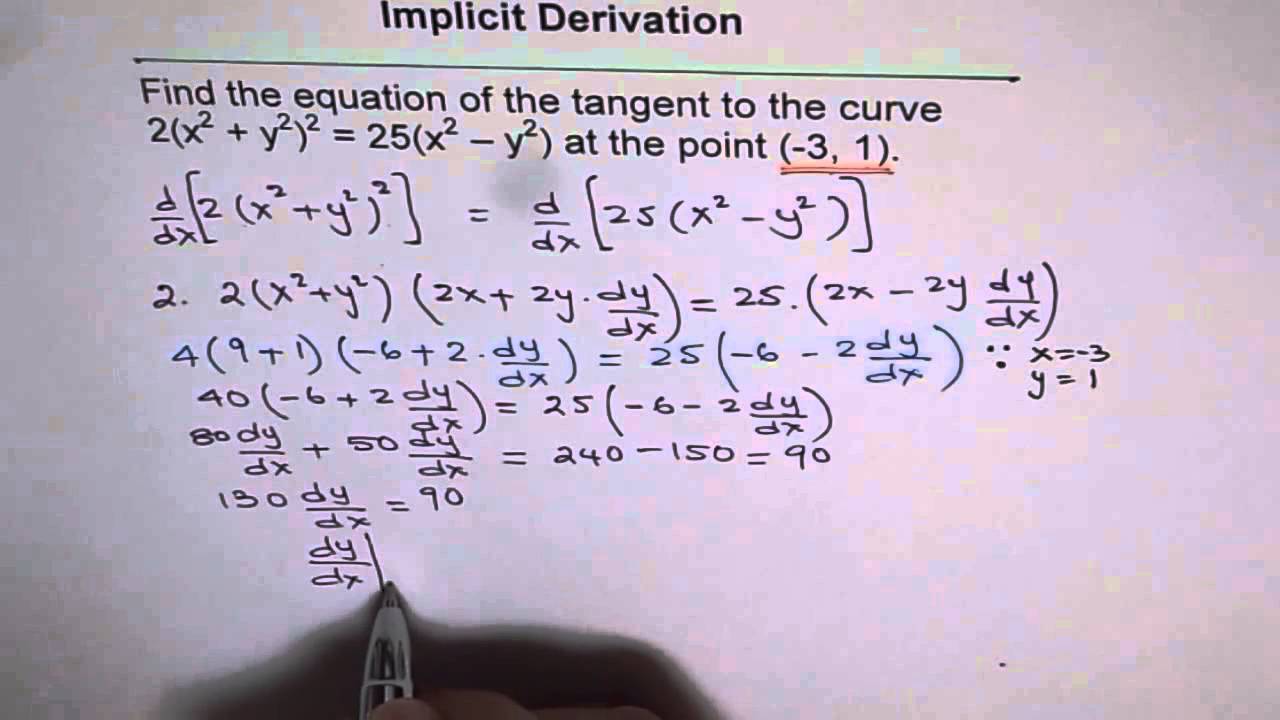



Equation Of Tangent To 2 X 2 Y 2 2 25 X 2 Y 2 Implicit Differentiation Youtube




Evaluate 81 36 X 2 Y 2 25 Brainly Com



0 件のコメント:
コメントを投稿