I did develop the formula using the 3 steps shown in the graphic I describe them bellowAgain, Fig 1 is y = f(x) Its reflection about the xaxis is y = −f(x) Every yvalue is the negative of the original f(x) Fig 3 is the reflection of Fig 1 about the yaxis Every point that was to the right of the origin gets reflected to the left And every point that was onVertical reflection can be defined as the reflection which is along the X coordinate axis and all the values of y coordinate axis are flipped to other part vertically without making any changes in the values of x coordinate axis If f (x) is a function then its vertical reflection can be represented as y=f (x)

What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic
Reflection over y x formula
Reflection over y x formula-(x, y) → (x 5, y 3) y = 2x 4 → (y 3) = 2(x 5) 4 y 3 = 2x 10 4 y 3 = 2x 6 y = 2x 3This video shows reflection over the xaxis, yaxis, x = −3, y = 5, y = x, and y = − x Show Video Lesson Reflections using Matrices This lesson involves reflections in the coordinate plane We use coordinate rules as well as matrix multiplication to reflect a polygon (or polygon matrix) about the xaxis, yaxis, the line y = x or the



Assignment 2 Transforming Parabolas
5x6=3x8 \frac {3} {4}x\frac {5} {6}=5x\frac {125} {3} \sqrt {2}x\sqrt {3}=\sqrt {5} 7y53y1=2y2 \frac {x} {3}\frac {x} {2}=10 linearequationcalculator y=x 👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xA Formula to Reflect a Point in y = x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinates The image below shows a general Cartesian coordinate being reflected in the line y = x
Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x b m = − 1 m = 1 b = 0 b = 0A point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxisFor a point reflection, we actually reflect over a specific point, usually that point is the origin $ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red a , \red b) $ Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
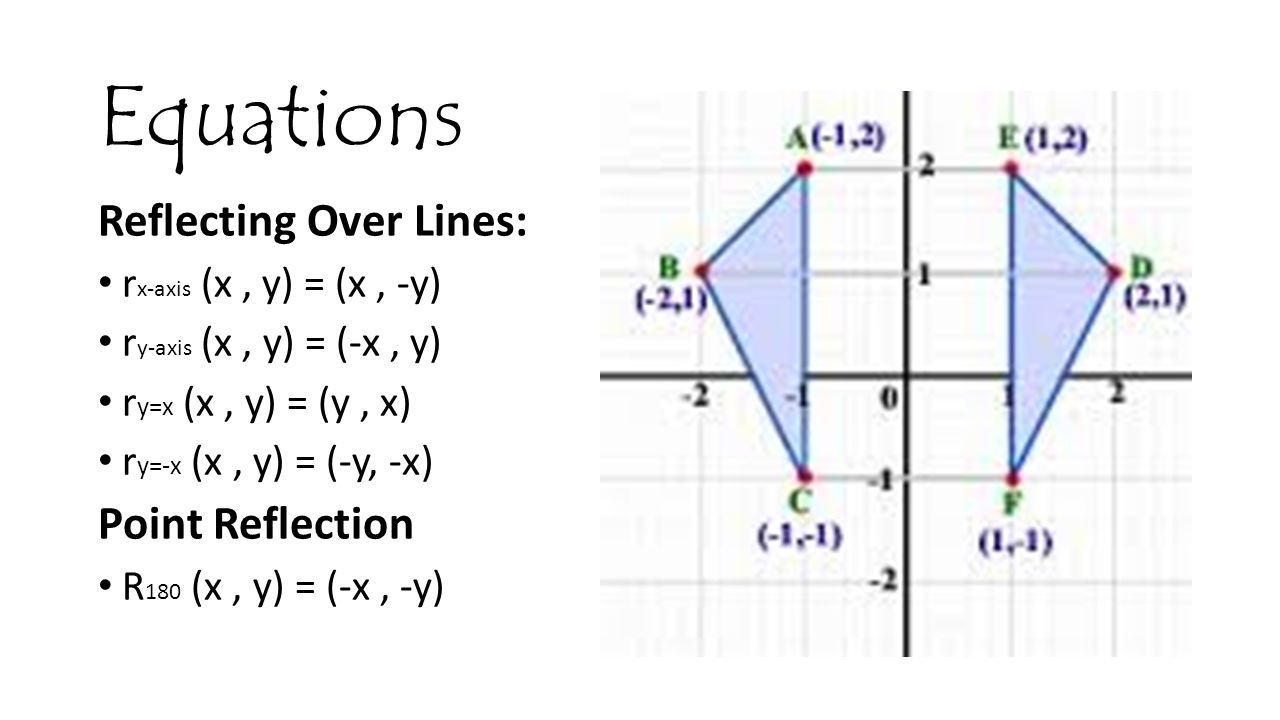
Over the line y = x (x, y) (y, x) Through the origin (x, y) (–x, –y) TRANSLATIONS Translations are a slide or shift Translations can be achieved by performing two composite reflections over parallel lines Translations are isometric, and preserve orientation Coordinate plane rules (x, y) (x ± h, y ± k) where h and k are theReflection in the line y=−x The rule for a reflection in the origin is (x,y)→(−y,−x) How do you reflect an equation over the y axis?Reflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflection




Reflection Rules How To W 25 Step By Step Examples




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor
Transcript We can reflect the graph of y=f (x) over the xaxis by graphing y=f (x) and over the yaxis by graphing y=f (x) See this in action and understand why itReflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABCReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $
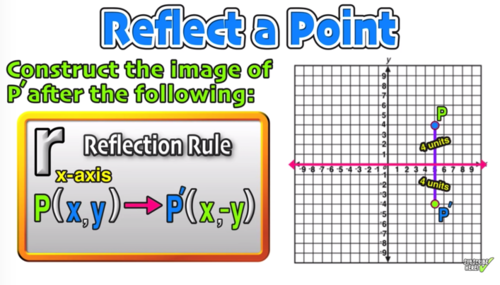



Reflection Over The X And Y Axis The Complete Guide Mashup Math
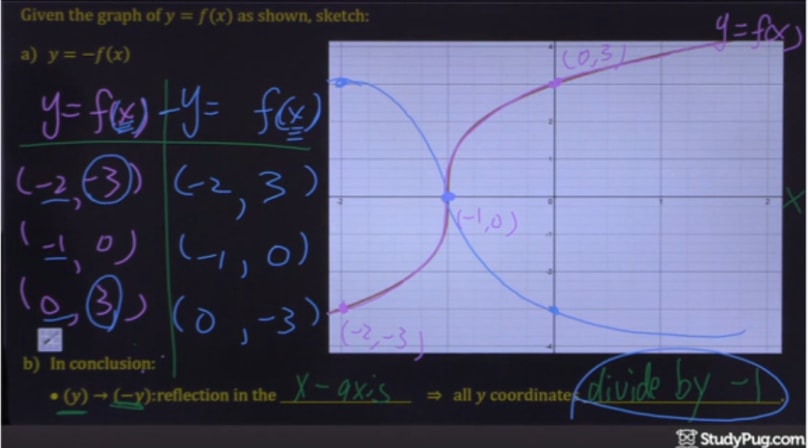



How To Reflect A Graph Through The X Axis Studypug
I was trying to understand how to calculate the reflection vector and found these answers I couldn't understand them easily, so I took my time to do it myself, the good thing is that I can now detail it in an ELI5 fashion!To flip or reflect (horizontally) about the vertical yaxis, replace y = f(x) with y = f(x)Answer (1 of 2) There are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joining PP′ is perpendicular to



Assignment 2 Transforming Parabolas




Reflection Over The Line Y X Math Showme
Key Points A vertical reflection is given by the equation y=−f(x) y = − f ( x ) and results in the curve being "reflected" across the xaxisAnswers A1 The transformation is the reflection in the vertical line with equation (normalsize {x=1}) This is reflection in the line (normalsize {y=x}), which passes through the origin (normalsize { 0,0}) and the point (normalsize { 1,1}) A3The line y = x is the point ( y, x ) Reflect over any line Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure The line of reflection will lie directly in the middle between the original figure and its image




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic



What Does It Mean To Reflect Over The Y X Line Quora
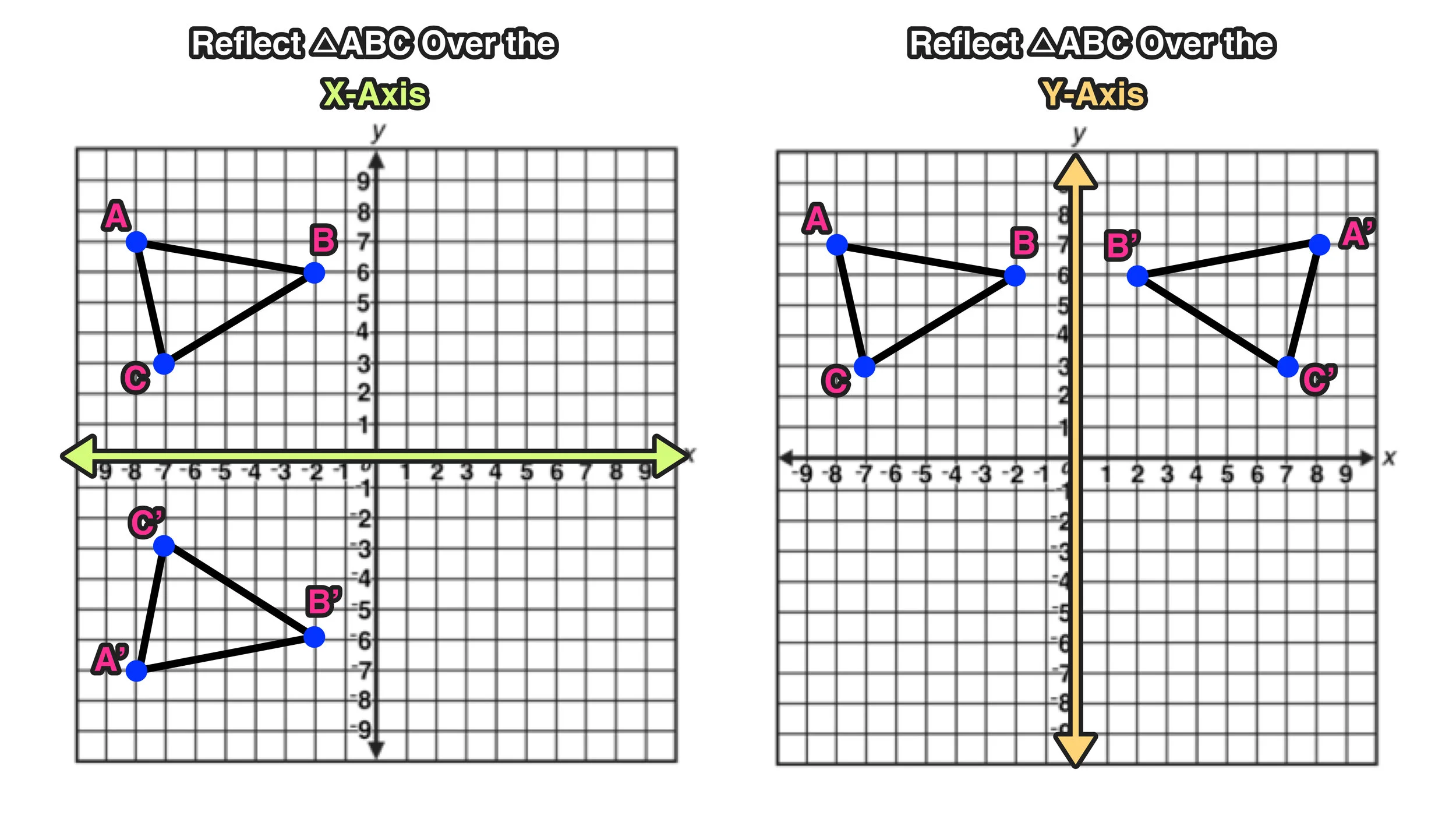
Given a function f ( x) \displaystyle f\left (x\right) f (x), a new function g ( x) = f ( − x) \displaystyle g\left (x\right)=f\left (x\right) g(x) = f (−x) is a horizontal reflection of the function f ( x) \displaystyle f\left (x\right) f (x), sometimes called a reflection about the y axisA reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a line of symmetry using a reflection matrixThe rule for a reflection over the y axis is ( x , y ) → ( − x , y ) Reflection in the line y = x A reflection of a point over the line y = x is shown
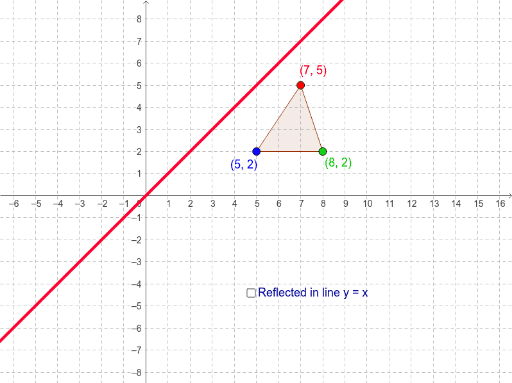



Reflection In The Line Y X Geogebra




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
Learn how to graph the linear equation of a straight line y = x using table methodLearn about reflection in mathematics every point is the same distance from a central line Show Ads Hide Ads About Ads into (x,−y) YAxis When the mirror line is the yaxis we change each (x,y) into (−x,y) Fold the Paper And when all else fails, just fold the sheet of paper along the mirror line and then hold it up to the light !Graphing Reflections In addition to shifting, compressing, and stretching a graph, we can also reflect it about the xaxis or the yaxisWhen we multiply the parent function latexf\left(x\right)={b}^{x}/latex by –1, we get a reflection about the xaxisWhen we multiply the input by –1, we get a reflection about the yaxisFor example, if we begin by graphing the parent



Reflection Of A Point In A Line Assignment Point
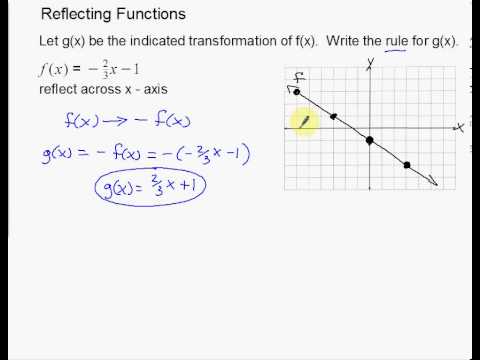



Linear Reflections Across X And Y Axis Example Youtube
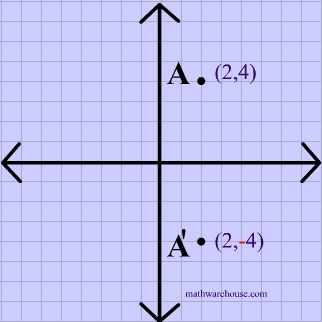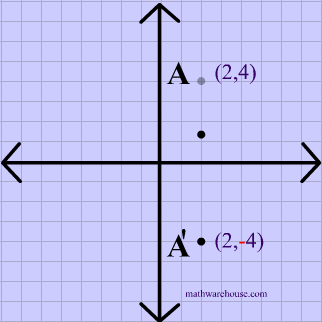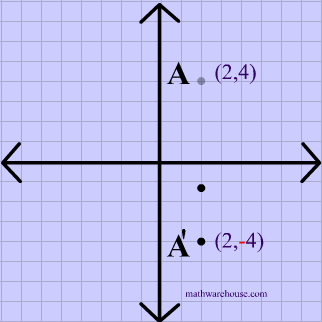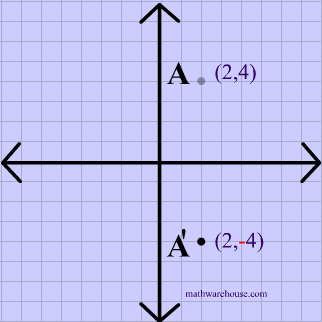
Reflection Definition In Geometry, a reflection is known as a flip A reflection is a mirror image of the shape An image will reflect through a line, known as the line of reflection A figure is said to be a reflection of the other figure, then every point in a figure is at equidistant from each corresponding point in another figure Reflecting a shape using x = a or y = b Answers 4 Downloadable version Horizontal and vertical reflections 5 Alternative versions feel Dividing decimals Dividing fractions Dividing negative numbers Dividing terms Drawing axes Enlargement Equation of a circle Equation of a straight line graph Equation of a tangent Equations fromThe line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 When reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x = (y,x) For example For triangle ABC with coordinate points A (3,3), B (2,1), and C (6,2), apply a reflection



Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis




Reflections How To Reflect A Point Reflect Point Across X Axis Y Axis And Other Lines Reflection Math 8th Grade Math Maths Activities Middle School
Rule Let y = f (x) be a function In the above function, if we want to do reflection through the yaxis, x has to be replaced by x and we get the new function y = f (x) The graph of y = f (x) can be obtained by reflecting the graph of y = f (x) through the yY = f (x) y = f (−x) Remember, the only step we have to do before plotting the f (x) reflection is simply divide the xcoordinates of easytodetermine points on our graph above by (1) When we say "easytodetermine points" what this refers to is just points for which you know the xSo, reflection in X axis means reflection in the line y = 0 Let P (x, y) be any point in the plane Draw a perpendicular PL from the point P to the X axis and produce it to the point P' such that PL = LP' Then P' is the image of P after reflection in X axis Here, coordinates of L are (x, 0)
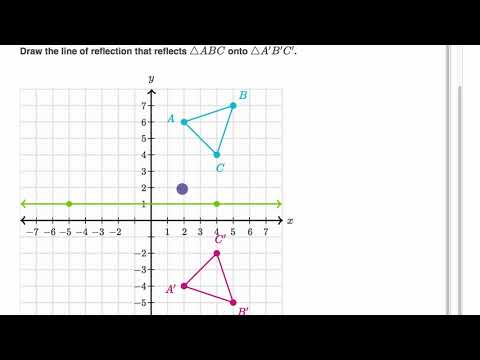



Determining Reflections Video Khan Academy




Reflections
We have reflected the shape in the line y = −x A Formula to Reflect a Point in y = −x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinates The rule for reflecting over the Y axis is to negate the value of the xcoordinate of each point, but leave the value the same For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)What is the formula for reflection Y = X?
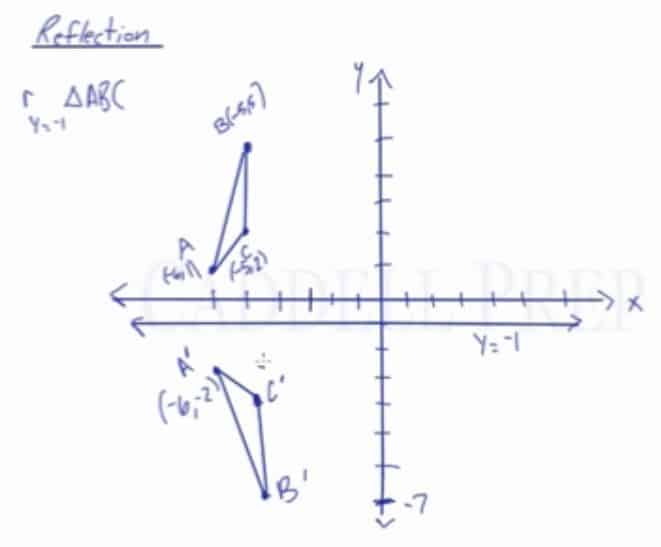



Learn About Reflection Over A Horizontal Or Vertical Line




Transformations Boundless Algebra
Answer (1 of 3) Hey Fam One of the most basic transformations you can make with simple functions is to reflect it across the yaxis or another vertical axis In a potential test question, this can be phrased in many different ways, so make sure you recognize the following terms as just anotherX y z In other words, The Tangential Electric Field is Continuous So E i (y= 0) E r (y= 0) = E t (y= 0) The component of the Efield that lies in the xz plane is continuous as you move across the plane of the interface Here, all Efields are in the zdirection, which is in the plane of the interface (We're not explicitly writing Reflection Over the XAxis For our first example let's stick to the very simple parent graph of y = x^2 {See video for graph} On the screen you can see that the graph of this equation is a parabola



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection What is the equation for reflection?Graph y=x Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Rewrite the equation as xintercept (s) in point form xintercept (s) xintercept (s) Find the yGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha




Reflecting Shapes Article Reflections Khan Academy




Reflection Over The Line Y X Youtube
Make y the subject of the formula 2y = x 1, so y = ½(x 1) Note that the graph of f1 will be the reflection of f in the line y = x This video explains more about the inverse of a function Graphs Functions can be graphed A function is continuous if its graph has no breaks in it An example of a discontinuous graph is y = 1/x, sinceQuadrant 1 (,) Quadrant 2 ( , ) Quadrant 3 (, ) Quadrant 4 (, ) 90 degree rotation 1)flip order of x and yReflect a line over y=x 1) new slope is reciprocal 2) point find intersecting point using systems of equations 3)yy1=m(xx1) and you get the equation!




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Which Point Would Map Onto Itself After A Reflection Across The Line Y X Maps Location Catalog Online




Solved The Graph Shown To The Right Involves A Reflection In Chegg Com




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Over The Y X Line Youtube




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Y X 2
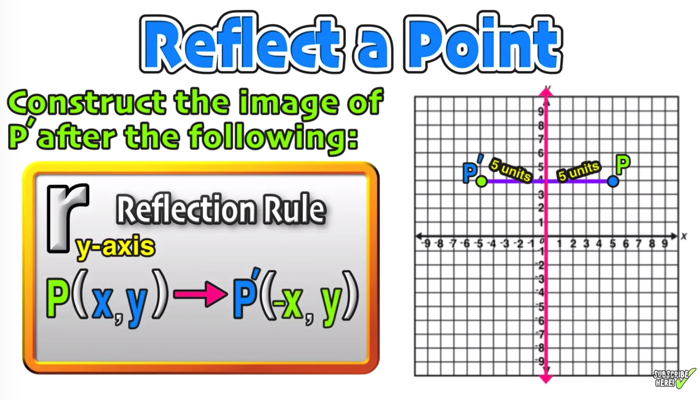



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Rules How To W 25 Step By Step Examples




Reflection Mathbitsnotebook A1 Ccss Math



1



Solution Describe The Relationship Between The Graph Of Y 2x 1 And It 39 S Reflection Across The Line Y X
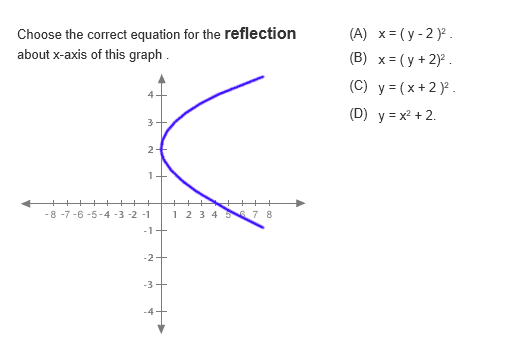



Solved Choose The Correct Equation For The Reflection About Chegg Com
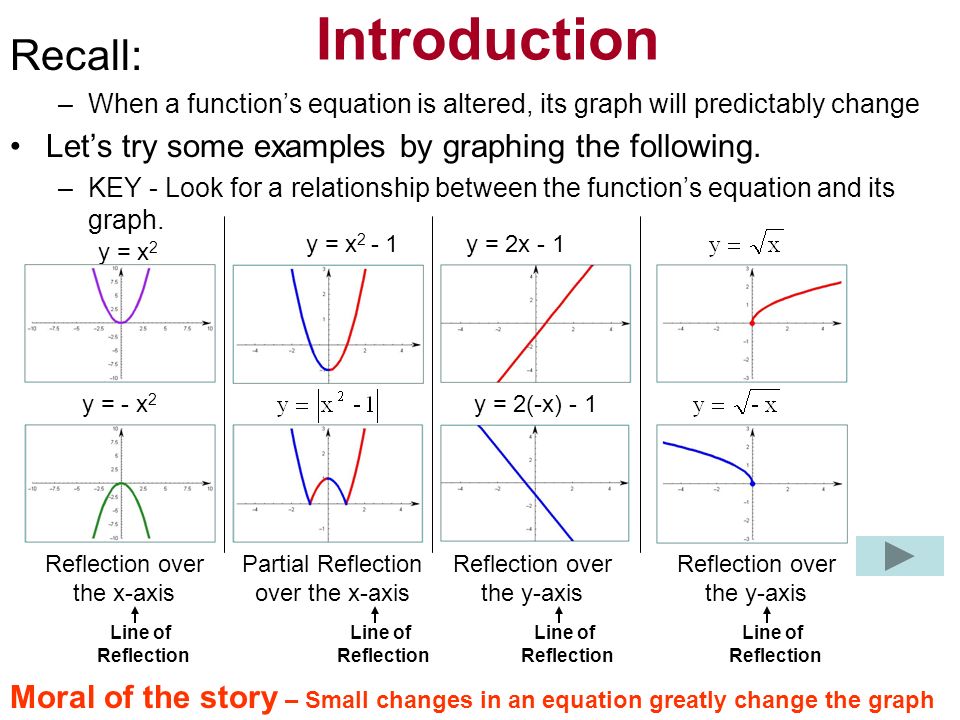



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download




Algebraic Representations Of Reflections




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Reflection Mathbitsnotebook A1 Ccss Math
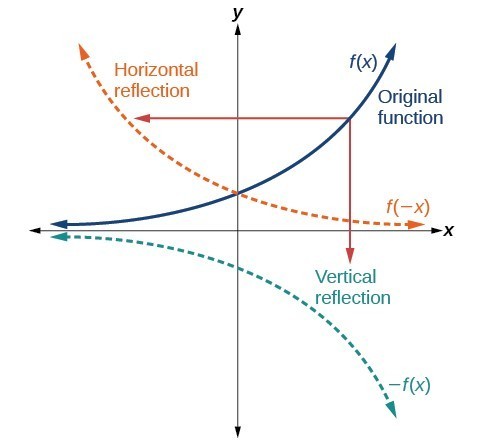



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




Reflection Transformation Matrix



How To Reflect A Graph Through The X Axis Studypug




The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange
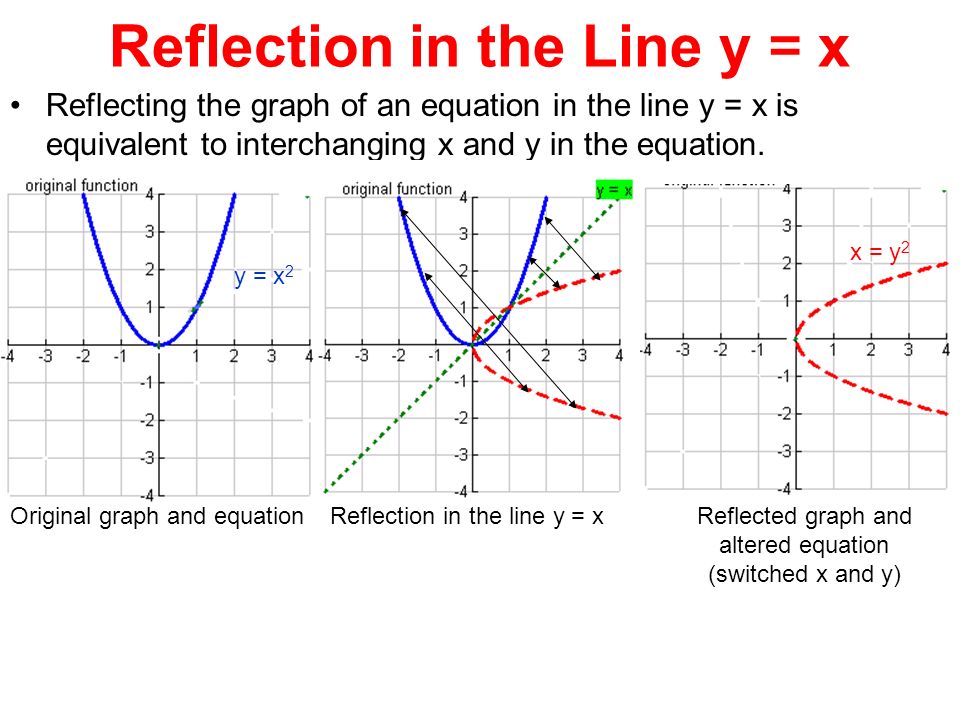



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
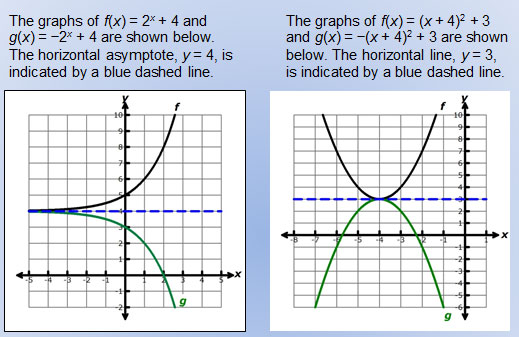



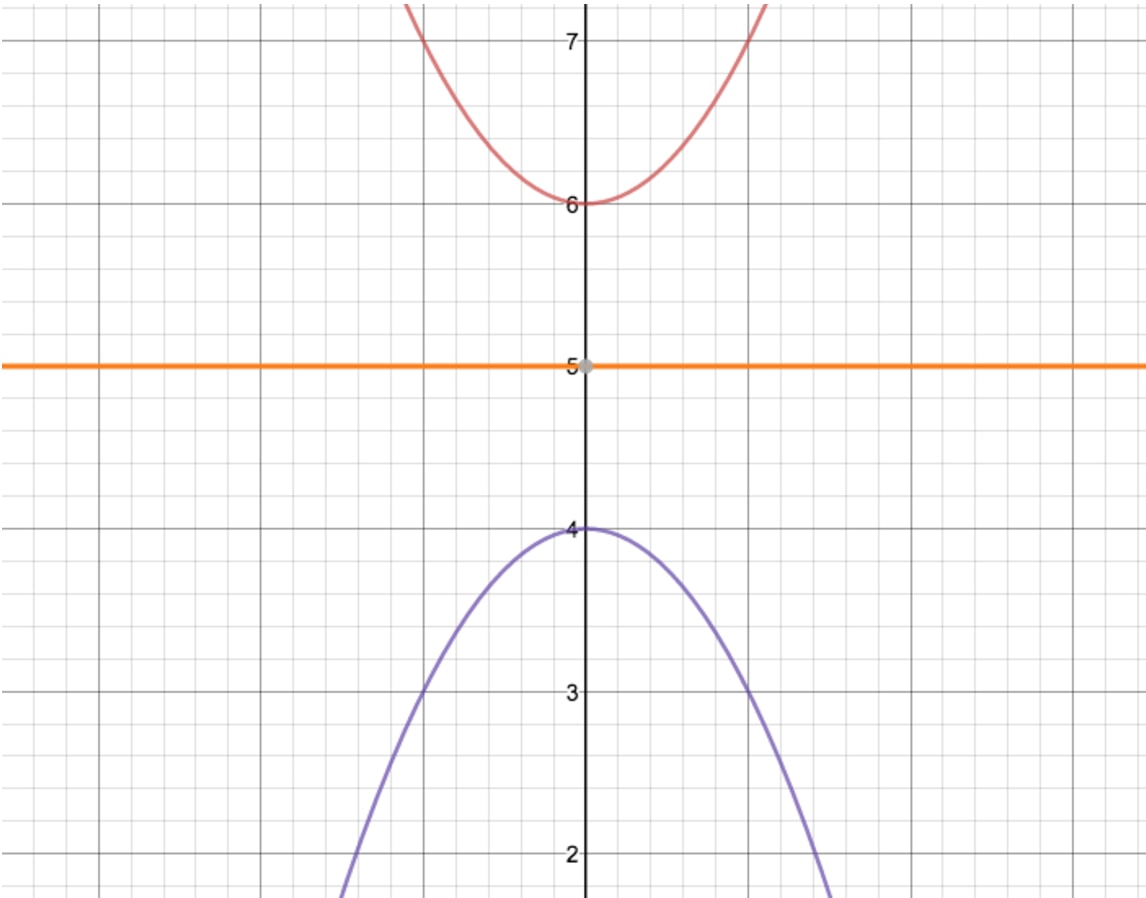
Untitled Document
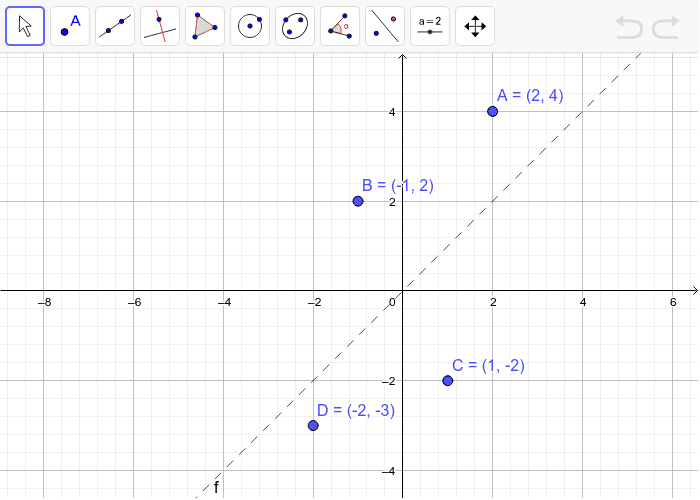



Reflecting In The Line Y X 2 Geogebra



Math Alive Geometry 1




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Transformation Matrix
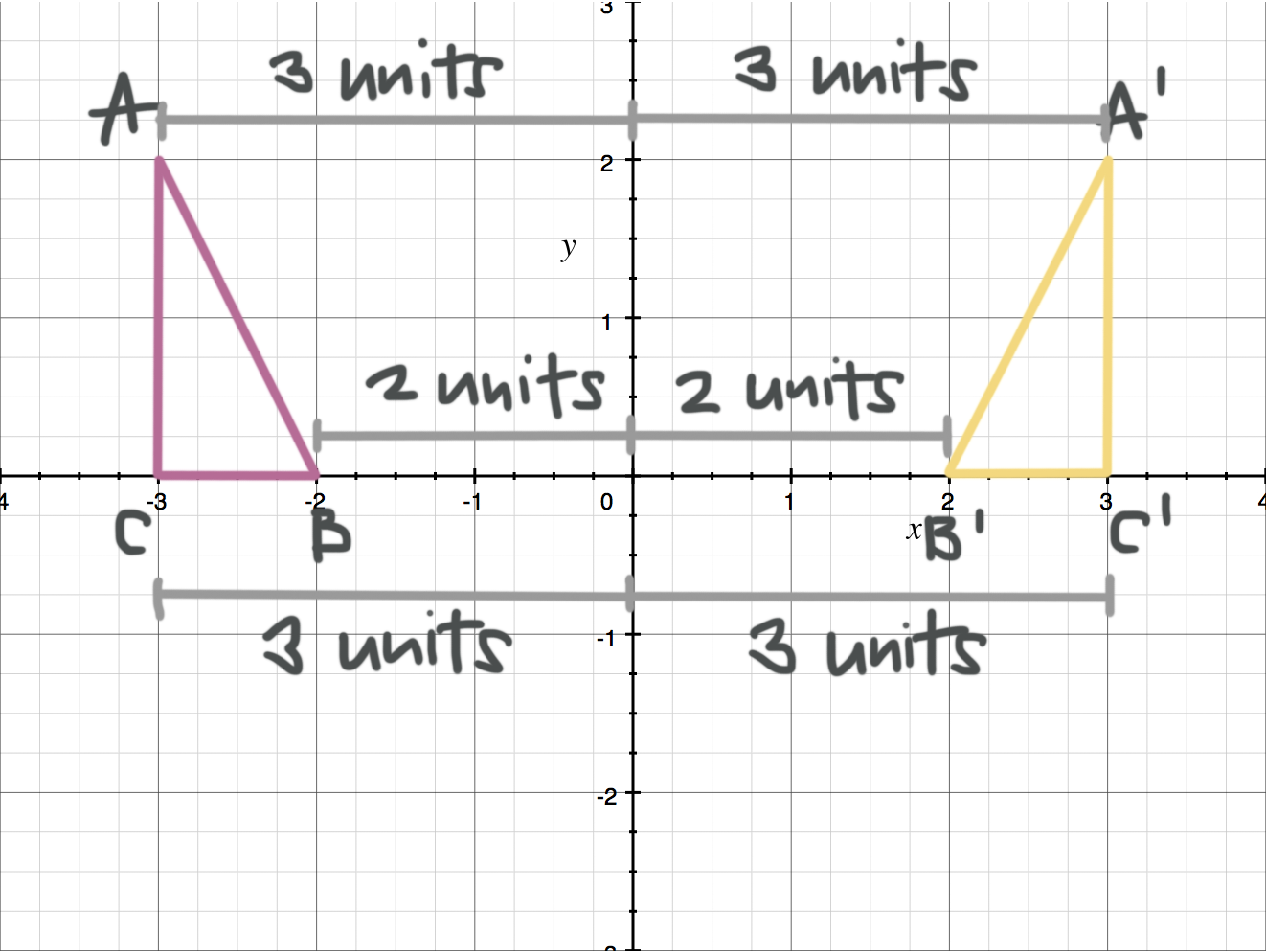



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflection Mathbitsnotebook A1 Ccss Math




Reflection Over Y 2 With Rule Educreations
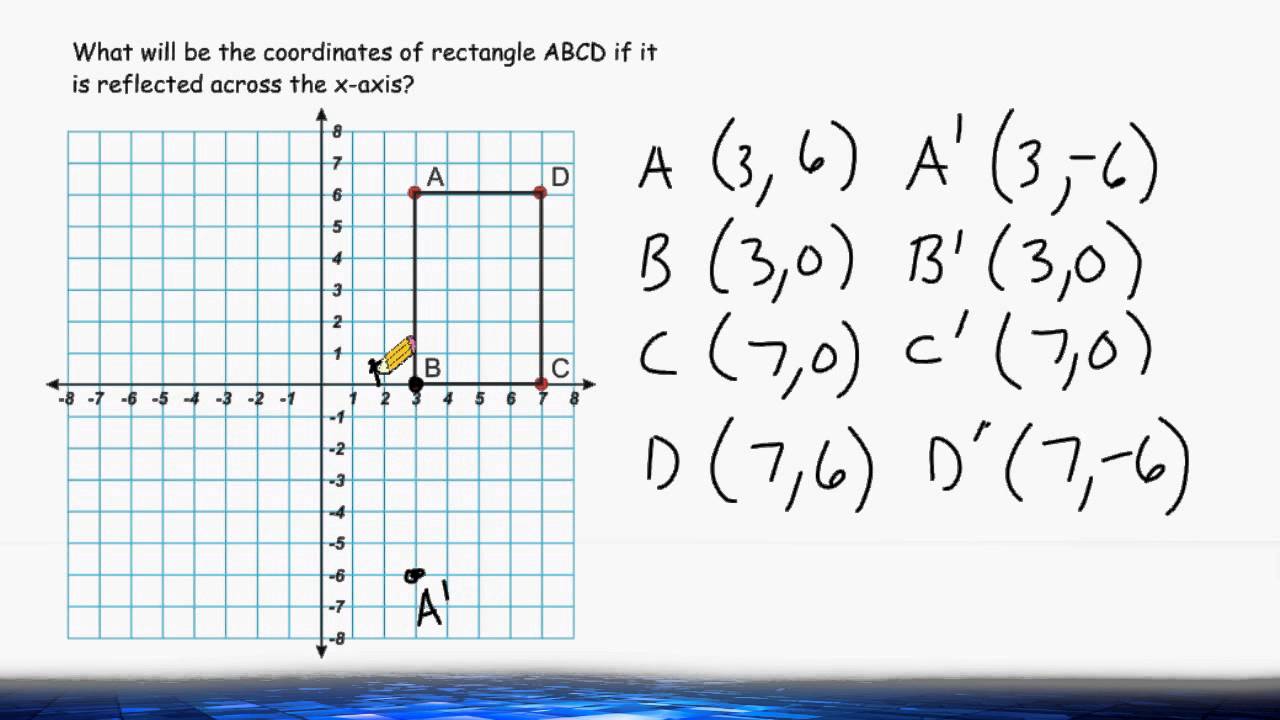



Transformations Reflection Across The X Axis Youtube




Solved This Question Involves Geometric Transformations Chegg Com



Math Alive Geometry 1




Transformation Reflection Over The Line Y X Youtube



1




Reflect Function About Y Axis F X Expii




Reflection In The Line Y X Transformation Matrix Youtube



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
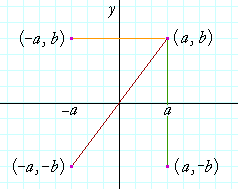



Reflections Of A Graph Topics In Precalculus
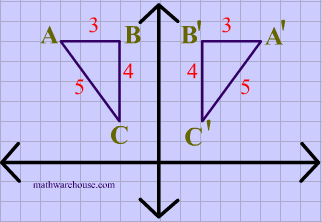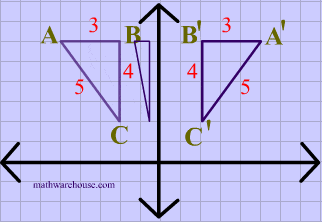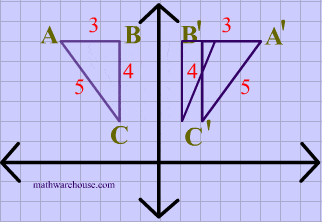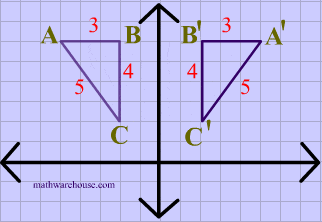



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Common Reflections Key Stage 3




Reflections Across Y X Geogebra
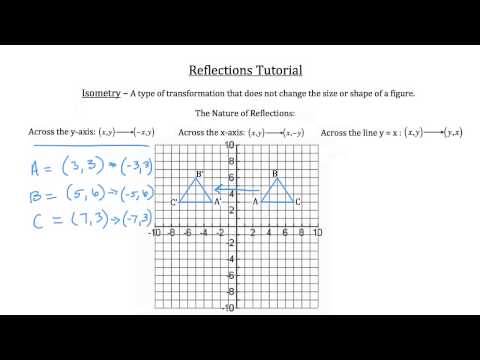



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs



Assignment 2 Transforming Parabolas




Reflection Definition Reflection In The Coordinate Plane




Reflecting Functions Examples Video Khan Academy



Reflect Function About Y Axis F X Expii




Picture Of Reflection In The Line Y X Reflection Math Common Myths Types Of Reflection




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
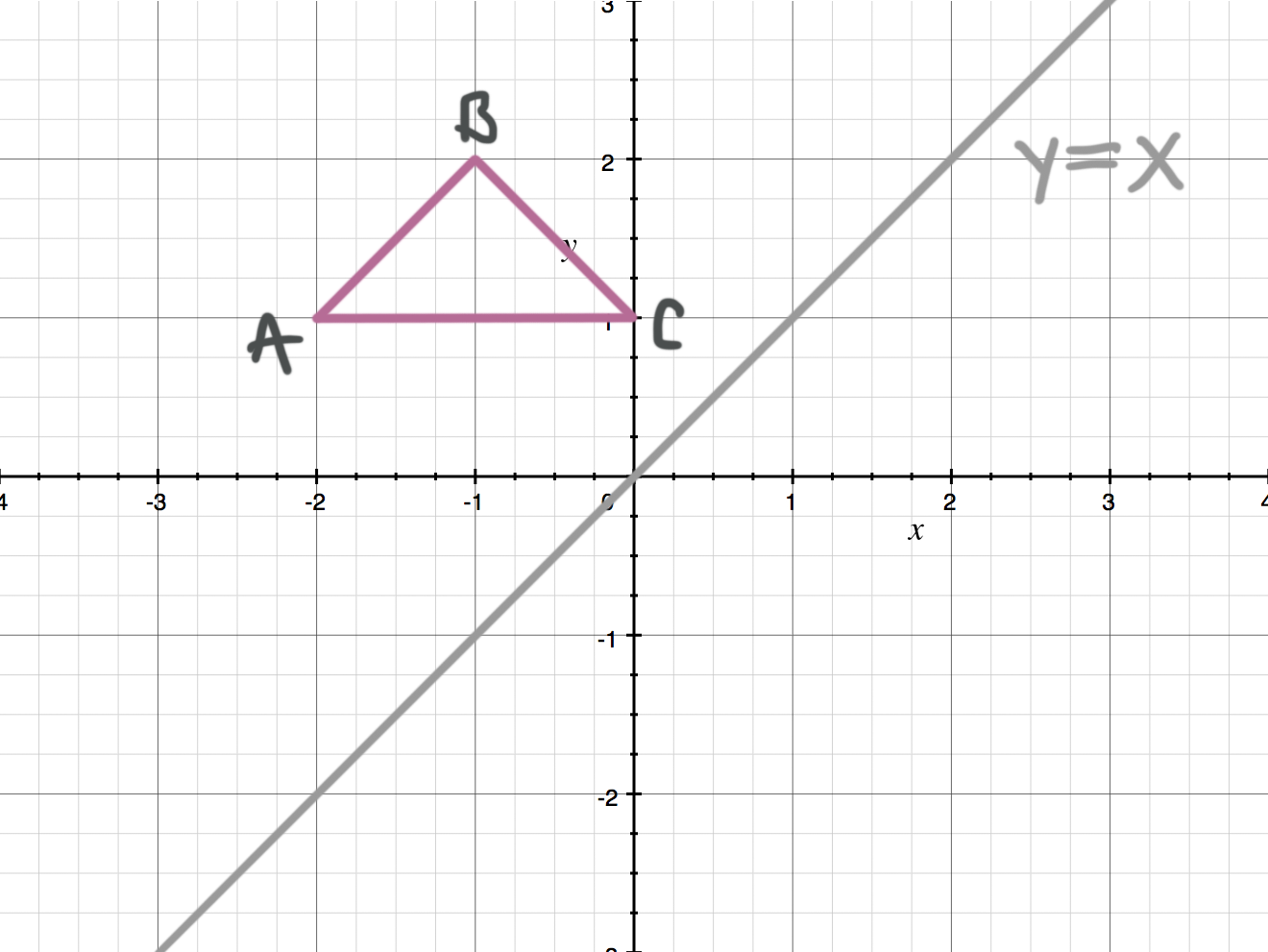



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q
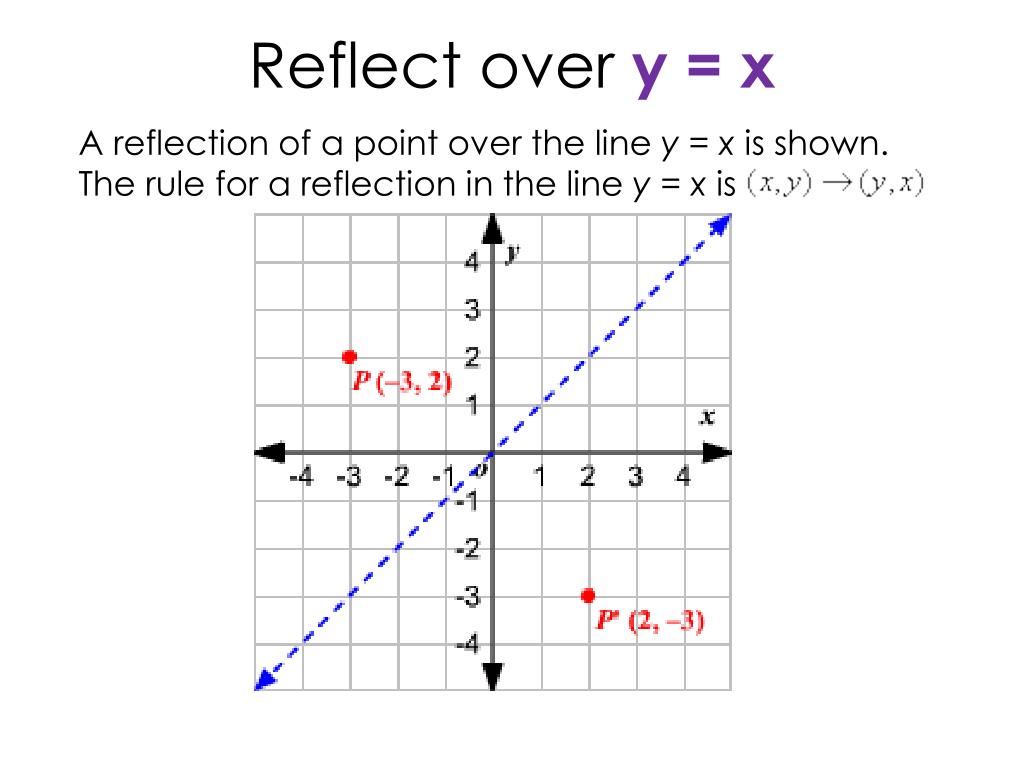



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id




Picture Of Reflection Across Y Axis Reflection Math Math Reflection




Reflection Over Y X Math Geometry Showme



What Is The Image Of 2 5 Reflected Across X 2 Socratic
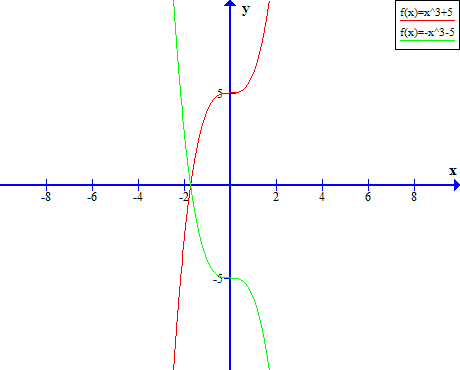



If The Graph Y X 3 5 Is Reflected In The X Axis What Is The New Equation Socratic
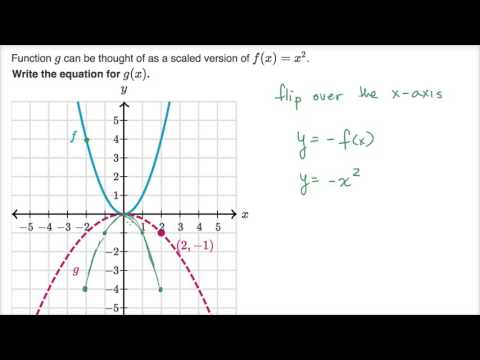



Scaling Reflecting Parabolas Video Khan Academy
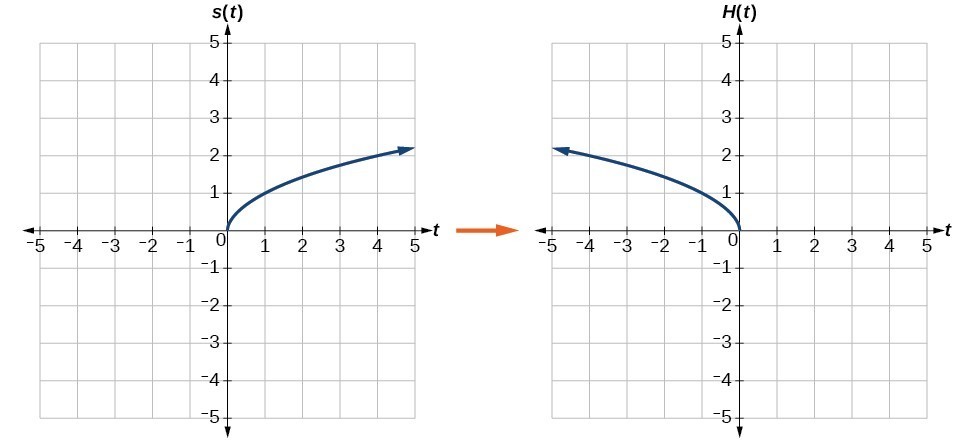



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation



Operations On Functions Reflections And Rotations Sparknotes




Learn About Reflection Over The Line Y X Caddell Prep Online




Reflection




How To Find A Reflection Image
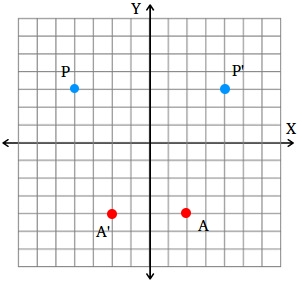



How To Find A Reflection Image




10 Math Problems Transformation Reflection



Does Reflecting The Parabola Across The X Axis Change The Axis Of Symmetry Quora
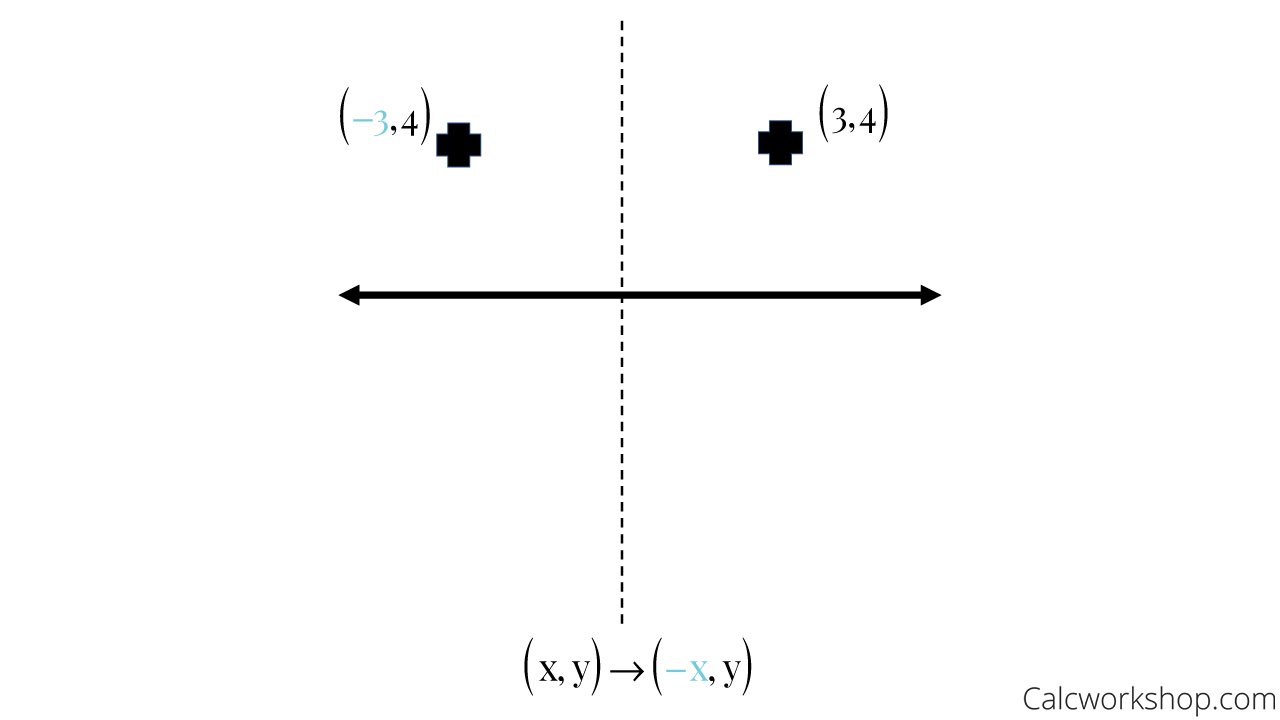



Reflection Rules How To W 25 Step By Step Examples




Describing A Reflection Key Stage 2




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Reflection Transformation Matrix




Reflection Over The Line Y X Geogebra




Reflection Rules How To W 25 Step By Step Examples



1




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
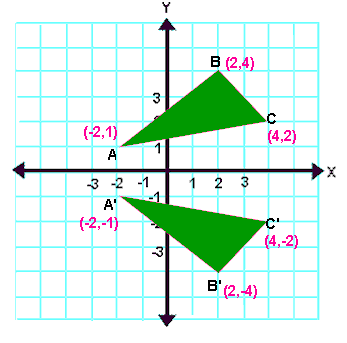



Reflection Transformation Matrix




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
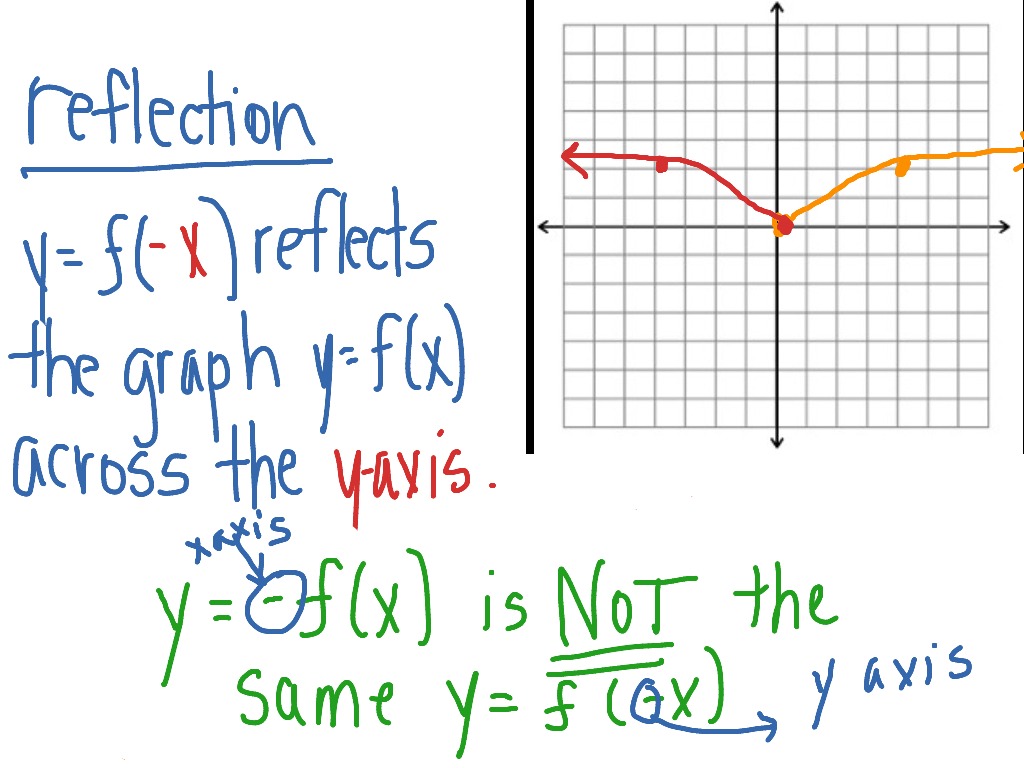



Reflection Across The Y Axis Math Functions Showme




Transformations Of Graphs



0 件のコメント:
コメントを投稿